Introduction

Example: For example, a spam filter can be used to classify emails as spam or not spam. A credit card fraud detection system can be used to classify transactions as legitimate or fraudulent.

Learners in Classification Problems

• Lazy Learners: In lazy learning, the algorithm initially stores the training dataset and then awaits the arrival of the test dataset. Classification is conducted using the most relevant data from the training dataset. While this approach reduces training time, it requires more time for predictions. Examples of lazy learning algorithms include case-based reasoning and the k-Nearest Neighbors (KNN) algorithm.
• Eager Learners: Eager learners construct a classification model using the training dataset before obtaining a test dataset. They invest more time in studying the data and less time in making predictions. Examples of eager learning algorithms include Artificial Neural Networks (ANN), naive Bayes, and Decision Trees.

Classification Predictive Modeling

• Think of sorting emails as either spam or not spam.
• Imagine recognizing handwritten characters, like letters or digits.
• Consider deciding if a user's behavior indicates they might stop using a service (churn).

1. Binary Classification: Sorting into two categories, like spam or not spam. Binary classification problems often require two classes, one representing the normal state and the other representing the aberrant state. For instance, the normal condition is "not spam," while the abnormal state is "spam." Class label 0 is given to the class in the normal state, whereas class label 1 is given to the class in the abnormal condition. A model that forecasts a Bernoulli probability distribution for each case is frequently used to represent a binary classification task.
   Let \(X\) be a normal variable representing the input features, and \(y\) be a binary random variable representing the class label (0 or 1). The Bernoulli distribution models the probability of success (or the positive outcome, often denoted as \(p\)) in a single Bernoulli trial. The probability mass function (PMF) of the Bernoulli distribution is given by: $$P(y=1|X) = p$$ $$P(y=0|X) = 1-p$$ Here \(p\) represents the probability of the positive outcome given the input features \(X\). (For more details, see Descriptive statistics.)
   The following are well-known binary classification algorithms:
   • Logistic Regression
   • Support Vector Machines
   • Simple Bayes
   • Decision Trees
2. Multi-Class Classification: Sorting into several categories, like different types of animals. The multi-class classification does not have the idea of normal and abnormal outcomes, in contrast to binary classification. Instead, instances are grouped into one of several well-known classes. In some cases, the number of class labels could be rather high. In a facial recognition system, for instance, a model might predict that a shot belongs to one of thousands or tens of thousands of faces. Text translation models and other problems involving word prediction could be categorized as a particular case of multi-class classification. Multiclass classification tasks are frequently modeled using a model that forecasts a Multinoulli probability distribution for each example.
   A Multinoulli probability distribution, also known as a categorical distribution, is a generalization of the Bernoulli distribution to more than two categories. Instead of having just two possible outcomes (e.g., 0 and 1), a Multinoulli distribution accommodates multiple discrete outcomes, each with its own probability. Mathematically, let \(X\) be a random variable representing the input features, and \(y\) be a categorical random variable representing the class label among \(K\) possible categories (where \(K\) is greater than 2). The Multinoulli distribution models the probability of each category \(k\) in a single trial. The probability mass function (PMF) of the Multinoulli distribution is given by: $$P(y=k|X) = p_k$$ where \(p_k\) represents the probability of category \(k\) given the input features \(X\), and \(\sum_{k=1}^K p_k = 1\) (since the probabilities must sum up to 1 for all possible categories). (For more details, see Descriptive statistics.)
   For multi-class classification, many binary classification techniques are applicable. The following well-known algorithms can be used for multi-class classification:
   • Progressive Boosting
   • Choice trees
   • Nearest K Neighbors
   • Rough Forest
   • Simple Bayes
   In multi-class classification tasks, the "one-vs-rest" (OvR) and "one-vs-one" (OvO) methods are commonly used.
   • One-vs-Rest (OvR): Also known as "one model for each class," this method involves training multiple binary classification models, each classifying one class against all other classes.
   • One-vs-One (OvO): In this approach, a binary classifier is trained for each pair of classes. This results in \(\frac{N\times (N-1)}{2}\) classifiers for \(N\) classes.
3. Multi-Label Classification: Multi-label classification involves predicting two or more class labels for each example, unlike multi-class or binary classification, where only one label is predicted. For example: tagging a post with multiple topics, or in photo classification, a model might predict the presence of multiple objects like "person," "apple," and "bicycle" in a single image, as opposed to just one label.

   Multi-label classification problems are often addressed using models that predict multiple outcomes, treating each prediction as a binary classification. This means each label is predicted independently, similar to a Bernoulli probability distribution.

   Specialized versions of conventional classification algorithms, such as
   • Multi-label Gradient Boosting,
   • Multi-label Random Forests, and
   • Multi-label Decision Trees
   are used for multi-label classification tasks.

Difference between the Multi-class and Multi-Label classification models:

In multi-class classification, each example is assigned to one and only one class label from a set of two or more mutually exclusive classes. The goal is to predict the single most appropriate class label for each instance. Examples include predicting the species of a flower from among several categories (e.g., iris, daisy, rose) or classifying emails into different folders (e.g., work, personal, promotions). Only one class label is assigned to each instance.

In multi-label classification, each example can be assigned to multiple class labels simultaneously. The model predicts the presence or absence of each label independently for every instance. This approach is suitable for problems where instances may belong to multiple classes at the same time. For example, in image classification, a single image may contain multiple objects (e.g., person, dog, car), and the model needs to identify all of them. Multiple class labels can be assigned to each instance.

4. Imbalanced Classification: Dealing with datasets where one category is much more common than the others. Imbalanced classification refers to a scenario in machine learning where the distribution of class labels in the dataset is highly skewed, with one class significantly outnumbering the others. This can pose challenges for predictive modeling, as the model may become biased towards the majority class and perform poorly on the minority class(es). Addressing imbalanced classification typically involves techniques such as:
   • Resampling: This involves either oversampling the minority class, undersampling the majority class, or a combination of both to rebalance the dataset.
   • Algorithmic Approaches: Some algorithms are specifically designed to handle imbalanced datasets better, such as ensemble methods like Random Forests and Gradient Boosting, as well as various techniques like cost-sensitive learning and anomaly detection.
   • Evaluation Strategies: Choosing appropriate evaluation metrics that are sensitive to the imbalance, such as precision, recall, and F1-score, can provide a more nuanced understanding of the model's performance.

Types of Classification Algorithms

1. Logistic regression: A linear model used for binary classification. It estimates the probability that an instance belongs to a particular class based on its features. Despite its name, logistic regression is a classification algorithm rather than a regression algorithm.
2. Decision trees: A tree-like model where each internal node represents a feature, each branch represents a decision based on that feature, and each leaf node represents a class label. Decision trees are easy to interpret and can handle both numerical and categorical data.
3. K-nearest neighbors (KNN): A non-parametric, instance-based learning algorithm used for both classification and regression tasks. KNN classifies instances based on their similarity to nearby instances in the feature space. It is simple but computationally expensive for large datasets.
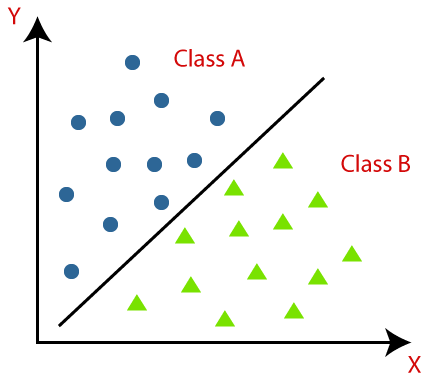
4. Support vector machines (SVMs) : A supervised learning algorithm that separates instances into different classes by finding the hyperplane that maximizes the margin between classes. SVMs are effective in high-dimensional spaces and are versatile due to their kernel trick, which allows them to handle nonlinear data.
5. Random Forest Algorithm: An ensemble learning method that constructs a multitude of decision trees during training and outputs the mode of the classes (classification) or the mean prediction (regression) of the individual trees. Random forests are robust against overfitting and can handle high-dimensional data.
6. Naive Bayes: A probabilistic classifier based on Bayes' theorem with the "naive" assumption of independence between features. It is simple and efficient, making it suitable for large datasets. Naive Bayes classifiers are often used for text classification tasks.

References

• My github Repositories on Remote sensing Machine learning
• A Visual Introduction To Linear regression (Best reference for theory and visualization).
• Book on Regression model: Regression and Other Stories
• Book on Statistics: The Elements of Statistical Learning
• https://www.colorado.edu/amath/sites/default/files/attached-files/ch12_0.pdf