K-Nearest Neighbors (KNN): Classification methods
Content
- Introduction
- Principle of KNN
- Distance metrics for k-nearest neighbours
- When Do We Use the KNN Algorithm?
- Steps to Effective K-Nearest Neighbors (KNN) Algorithm Implementation
- What value should you choose for k in k-nearest neighbours
- Why Do We Need the KNN Algorithm?
- Pros of using KNN
- Cons of Using KNN
- Example
- Reference
Introduction
- K-Nearest Neighbors (KNN) is a simple yet powerful supervised machine learning algorithm used for classification and regression tasks.
- It is a non-parametric and instance-based learning algorithm, meaning it doesn't make any underlying assumptions about the distribution of data and learns directly from the training instances.
- The main objective of the KNN algorithm is to predict the classification of a new sample point based on data points that are separated into several individual classes. It is used in text mining, agriculture, finance, and healthcare.
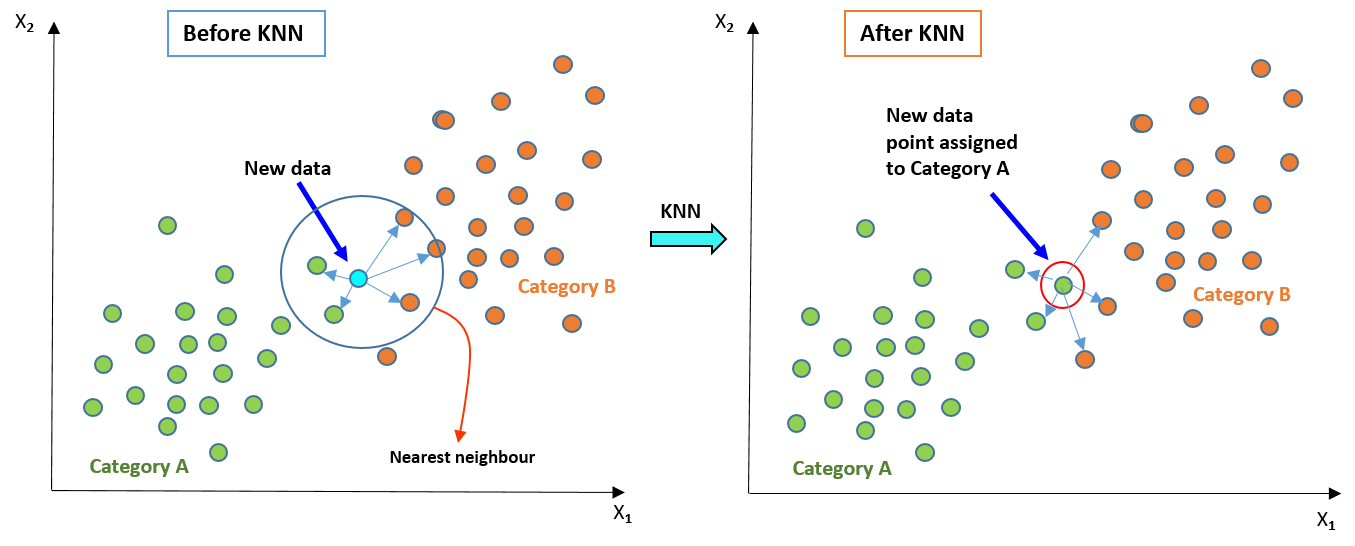
Principle of KNN
The principle behind KNN is straightforward: objects are classified based on the majority class among their K nearest neighbors. In other words, the class label of an unseen data point is determined by the class labels of its K nearest neighbors in the feature space.
- The central idea behind KNN is to classify a new data point based on the majority class of its nearest neighbors.
- It assumes that similar things are close to each other. Hence, if most of the nearest neighbors of a data point belong to a certain class, the new data point is likely to belong to that class as well
- Let use suppose that we have a set of training observations \((x,y)\) and they capture the relationship between \(x\) and \(y\). Now our goal is to make a model and then predict the values on the basis of new datasets.
- In the context of \(K\)-Nearest Neighbors (KNN), our goal is to learn a function \(h : X \rightarrow Y\) that can predict the output \(y\) for an unseen observation \(x\) based on the relationships between the input features \(X\) and the corresponding output labels \(Y\) in a labeled dataset.
- In the K-Nearest Neighbors (KNN) algorithm, \(K\) represents the number of nearest neighbors to consider when making predictions for a new data point.
- When a new data point is to be classified, KNN calculate the distances between the point and all other points in the dataset. It then selects the \(K\) nearest neighbors based on these distances. The class label or value assigned to the new data point is typically determined by the majority class or avergae value among these \(K\) nearest neighbors.
- The choice of \(K\) is crucial in KNN, as it significantly impacts the performance of the algorithm. A smaller \(K\) value may lead to more flexible decision boundaries, potentially capturing noise in the data but being more sensitive to outliers. On the other hand, a larger \(K\) value may provide smoother decision boundaries but might not capture local patterns effectively.
- Selecting an appropriate \(K\) value often involves experimentation and validation using techniques such as cross-validation to ensure optimal performance for the specific dataset and problem at hand.
Distance metrics for k-nearest neighbours
Distance metrics are crucial in the k-Nearest Neighbours (KNN) algorithm, as they determine how similarity or dissimilarity between data points is measured. The choice of distance metric can significantly impact the performance of the KNN algorithm. Here are some standard distance metrics used in KNN:
- Euclidean Distance: The most commonly used distance metric in KNN. Calculates the straight-line distance between two points in the feature space. Suitable for continuous numerical features.
Formula:
$$d(\vec{p},\vec{q}) = \sqrt{\sum_{i=1}^n (p_i - q_i)^2}$$The Euclidean distance measures the straight-line distance between two points in a Euclidean space and the formula calculates the square root of the sum of squared differences between corresponding coordinates of two points.
- Manhattan Distance (Taxicab or City Block Distance): Calculates the distance between two points by summing the absolute differences between their coordinates along each dimension. Practical when dealing with features measured in different units.
Formula:
$$d(\vec{p},\vec{q}) = \sum_{i=1}^n |p_i - q_i|$$Manhattan distance calculates the distance between two points by summing the absolute differences of their coordinates. It represents the distance a taxicab would travel to reach the destination by moving along the grid-like city blocks.
- Minkowski Distance: Minkowski distance is a generalization of both Euclidean and Manhattan distances.
Formula:
$$d(\vec{p},\vec{q}) = \left(\sum_{i=1}^n |p_i - q_i|^{r}\right)^{1/r}$$where The parameter 'r' controls the degree of the distance metric. When \(r=1\), it reduces to the Manhattan distance, and when \(r=2\), it becomes the Euclidean distance.
- Chebyshev Distance (Maximum Metric):
Chebyshev distance calculates the maximum absolute difference between the coordinates of two points.
Formula:
$$d(\vec{p},\vec{q}) = \max_{i}(|p_i - q_i|)$$It represents the distance a king would travel on a chessboard to move between two squares.
- Hamming Distance (for categorical data): Hamming distance measures the number of positions at which the corresponding symbols are different between two strings of equal length.
Formula:
$$d(\vec{p},\vec{q}) = \sum_{i=1}^n \delta(p_i \neq q_i)$$ It's commonly used for categorical variables or binary data. - Cosine Similarity: The Cosine Similarity is a metric used to measure the similarity between two vectors in a multidimensional space. It calculates the cosine of the angle between the two vectors, providing a measure of how closely the vectors align in direction, irrespective of their magnitude. The Cosine Similarity ranges from -1 to 1.
Formula:
$$\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \cdot \|\mathbf{b}\|}$$ where:- \(\mathbf{a} \cdot \mathbf{b}\) represents the dot product of the two vectors.
- \(\|\mathbf{a}\|\) and \(\cdot \|\mathbf{b}\|\) represent the magnitudes (or norms) of the vectors \(a\) and \(b\), respectively.
The Cosine Similarity is widely used in text analysis, document clustering, recommendation systems, and many other applications where vector representations are used to measure similarity between entities.
- Correlation Distance: Correlation distance is a measure of dissimilarity between two vectors that takes into account the correlation between their elements. It quantifies how much two vectors deviate from being perfectly positively correlated (correlation coefficient of 1) or perfectly negatively correlated (correlation coefficient of -1). The correlation distance ranges from 0 to 2, where:
- If the correlation coefficient is 1 (perfect positive correlation), the correlation distance is 0.
- If the correlation coefficient is -1 (perfect negative correlation), the correlation distance is 2.
Formula:
The formula for calculating the correlation distance between two vectors \(\vec{x}\) and \(\vec{y}\) of length \(n\) is given by $$\text{Correlation Distance}(\vec{x}, \vec{y}) = 1- \text{Correlation Coefficient}(\vec{x}, \vec{y})$$ where:- The correlation coefficient Correlation Coefficient(\(x\),\(y\)) measures the strength and direction of the linear relationship between the elements of vectors \(x\) and \(y\).
- The correlation distance is calculated as 1 minus the correlation coefficient to convert the correlation coefficient into a distance metric.
When Do We Use the KNN Algorithm?
The K-Nearest Neighbors (KNN) algorithm is used in various scenarios where its characteristics align well with the requirements of the problem. Here are some common situations where KNN is often used:
- Data is labeled
- Data is noise-free
- Dataset is small, as KNN is a lazy learner
Steps to Effective K-Nearest Neighbors (KNN) Algorithm Implementation
The K-NN working can be explained on the basis of the below algorithm:- Step-1: (Data processing): Clean and preprocess your dataset to handle missing values, outliers, and irrelevant features. Normalize or standardize the numerical features to ensure that all features contribute equally to the distance calculations.
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
# Assume X_train and X_test are your feature matrices
# Impute missing values
imputer = SimpleImputer(strategy='mean')
X_train_imputed = imputer.fit_transform(X_train)
X_test_imputed = imputer.transform(X_test)
# Standardize features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_imputed)
X_test_scaled = scaler.transform(X_test_imputed)
from sklearn.model_selection import train_test_split
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# Define KNN classifier
knn = KNeighborsClassifier()
# Define parameter grid
param_grid = {'n_neighbors': [3, 5, 7, 9, 11]}
# Perform grid search
grid_search = GridSearchCV(knn, param_grid, cv=5)
grid_search.fit(X_train, y_train)
# Get the best value of K
best_k = grid_search.best_params_['n_neighbors']
# By default, KNeighborsClassifier uses Euclidean distance
# You can specify different distance metrics using the 'metric' parameter
knn = KNeighborsClassifier(metric='manhattan')
# Using the best value of K obtained from grid search
knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train_scaled, y_train)
from sklearn.metrics import accuracy_score
# Make predictions on the testing set
y_pred = knn.predict(X_test_scaled)
# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
# Use grid search or randomized search to tune hyperparameters
# Example using grid search is shown in step 3
from sklearn.model_selection import cross_val_score
# Perform k-fold cross-validation
cv_scores = cross_val_score(knn, X_train_scaled, y_train, cv=5)
# Use feature selection techniques such as SelectKBest or PCA
from sklearn.feature_selection import SelectKBest
from sklearn.decomposition import PCA
# Example using SelectKBest
selector = SelectKBest(k=5)
X_train_selected = selector.fit_transform(X_train_scaled, y_train)
X_test_selected = selector.transform(X_test_scaled)
# Example using PCA
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)
# Use efficient data structures for nearest neighbor search
# By default, KNeighborsClassifier uses a brute-force algorithm
# For large datasets, you can use KD-trees or Ball trees for faster search
knn = KNeighborsClassifier(algorithm='kd_tree')
What value should you choose for k in k-nearest neighbours?
Choosing the correct value for k in the k-Nearest Neighbours (KNN) algorithm is a critical step, as it can significantly impact the model’s performance. Selecting an appropriate k value involves finding a balance between bias and variance. Here are a few approaches you can use to choose the optimal k value:
- Cross-Validation: Split your dataset into multiple folds (e.g., using k-fold cross-validation). For each fold, train the KNN model with different k values and evaluate its performance on the validation set. Calculate the average performance metric (e.g., accuracy) for each k value across all folds. Choose the k value that results in the best average performance.
- Odd vs. Even \(K\) values: Choose odd \(K\) values to avoid ties when classifying data points with an equal number of nearest neighbours from different classes. Using an odd k value prevents indecisiveness in classification.
- Elbow Method: Plot the performance metric (e.g., accuracy) as a function of different k values. Look for the point on the plot where the performance stabilizes or starts to decrease. This point resembles an “elbow.” This method helps you identify a value k that offers a good trade-off between bias and variance.
- Grid Search: Perform a grid search over a predefined range of k values. Train and evaluate the model for each k value in the range. Choose the k value that gives the best performance on a validation set.
- Domain Knowledge: Sometimes, domain knowledge can help you make an informed decision about the k value. For example, if you know that the problem is expected to have specific characteristics, you can choose a k value accordingly.
- Use Case-Specific Testing: Experiment with different k values and assess the model’s performance on a separate test dataset that wasn’t used during training. This approach helps you directly observe how different k values affect real-world predictions.
Why Do We Need the KNN Algorithm?
The K-Nearest Neighbors (KNN) algorithm is valuable in data science and analytics for several reasons:- Flexibility in Data Patterns: KNN is effective in recognizing patterns in data that might not follow a linear or parametric model. It can handle complex relationships between features and target classes, making it suitable for a wide range of datasets.
- Non-parametric Approach: Unlike some other algorithms that make assumptions about the underlying data distribution, KNN is non-parametric. It doesn't require the data to be normally distributed or have a specific shape, making it versatile and applicable in various domains.
- Handling Multi-Class Classification: KNN can handle multi-class classification problems with ease. By considering the majority class among the nearest neighbors, it can assign a class label to a new data point based on the distribution of classes in its vicinity.
- Adaptability to New Data: KNN is well-suited for online learning scenarios where new data points need to be incorporated into the existing model without retraining. Since KNN doesn't have a training phase and simply memorizes the training data, it can quickly adapt to changes in the dataset.
- Interpretability: KNN predictions are intuitive and easy to interpret. The class assigned to a new data point is based on the classes of its nearest neighbors, providing insights into why a particular prediction was made.
- Robustness to Noisy Data: KNN can handle noisy data and outliers reasonably well. Since it relies on the majority class among the nearest neighbors, outliers are less likely to significantly impact the classification results compared to some other algorithms.
- Simple Implementation: KNN is relatively easy to implement and understand, making it accessible to beginners in machine learning and pattern recognition. Its simplicity also allows for quick experimentation and prototyping.
Pros of using KNN
- Simplicity: KNN is easy to understand and implement, making it accessible to beginners in machine learning and data science.
- No Training Phase: KNN is a lazy learning algorithm, meaning it doesn't require a training phase. Instead, it memorizes the entire training dataset, making it efficient for online learning scenarios where new data points need to be incorporated without retraining.
- Versatility: KNN can be applied to both classification and regression tasks. It can handle complex relationships between features and target variables, making it suitable for a wide range of datasets.
- Non-parametric: KNN makes no assumptions about the underlying data distribution, making it robust to different types of data. It can capture complex patterns in the data without relying on predefined models.
- Interpretability: Predictions made by KNN are intuitive and easy to interpret. The class label or regression value assigned to a new data point is based on the majority class or average value of its nearest neighbors.
Cons of Using KNN
- Computational Complexity: As the size of the training dataset grows, the computational cost of KNN increases significantly. Calculating distances between the new data point and all existing data points in the training set can be time-consuming for large datasets.
- Memory Usage: Since KNN memorizes the entire training dataset, it requires storing all training instances in memory. This can be problematic for datasets with a large number of features or a high-dimensional feature space, leading to high memory usage.
- Prediction Time: KNN incurs a high prediction time during inference. For each new data point, KNN needs to calculate distances to all training instances and determine the nearest neighbors, which can be slow for real-time or latency-sensitive applications.
- Sensitivity to Irrelevant Features: KNN considers all features equally when calculating distances between data points. Irrelevant or noisy features can negatively impact the algorithm's performance and lead to suboptimal results.
- Need for Optimal K Value: The choice of the hyperparameter K significantly influences the performance of KNN. Selecting an inappropriate value of K can lead to overfitting or underfitting of the model, requiring careful tuning and validation.
- Curse of Dimensionality: KNN's performance can degrade in high-dimensional feature spaces due to the curse of dimensionality. As the number of dimensions increases, the Euclidean distance between data points becomes less meaningful, making it challenging to define nearest neighbors accurately.
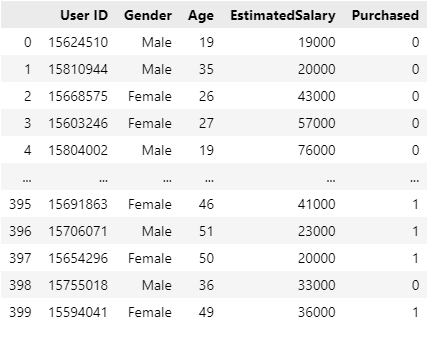
Example with the dataset on 'user_data.csv'
Again we consider the 'user_data.csv' used in Naive-Bayes algorithm (for the code, please see the github repository check the 'Project-2.3-KNN-classification.ipynb' file in the Github repo).
- Data loading:
# loading the important libraries
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
# loading the datset and creating a dataframe
df_user = pd.read_csv('User_Data.csv')
# Display the DataFrame
print(df_user.head())
# Importing the dataset
X = df_user.iloc[:, [2, 3]].values # features
y = df_user.iloc[:, 4].values # target
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
In next step, we fit the K-NN classifier to the training data. To do this we will import the KNeighborsClassifier class of the sklearn. The object Classifier from the KNeighborsClassifier which needs various parameters such as (formmore details, see the official documentation Sklearn.neighbors.KNeighborsClassifier):
n_neighbors: defines the required neighbors of the algorithm.metric='minkowski': This is the default parameter and it decides the distance between the points.p=2: It is equivalent to the standard Euclidean metric.
#Fitting K-NN classifier to the training set
from sklearn.neighbors import KNeighborsClassifier
classifier= KNeighborsClassifier(n_neighbors=5, metric='minkowski', p=2)
classifier.fit(X_train, y_train)
#Predicting the test set result
y_pred= classifier.predict(x_test)
#Creating the Confusion matrix
from sklearn.metrics import confusion_matrix
cm= confusion_matrix(y_test, y_pred)
cm
array(
[[64 4]
[ 3 29]], dtype=int64
)
# Importing libraries
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# Set up the figure with two subplots in one row and two columns
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# Visulaizing the training set result
x_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start=x_set[:, 0].min() - 1, stop=x_set[:, 0].max() + 1, step=0.01),
np.arange(start=x_set[:, 1].min() - 1, stop=x_set[:, 1].max() + 1, step=0.01))
axes[0].contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha=0.75, cmap=ListedColormap(['#87CEEB', '#90EE90']))
axes[0].set_xlim(X1.min(), X1.max())
axes[0].set_ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
axes[0].scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
c=ListedColormap(['#0000FF', '#2ca02c'])(i), label=j)
axes[0].set_title('K-NN Algorithm (Training set)')
axes[0].set_xlabel('Age')
axes[0].set_ylabel('Estimated Salary')
axes[0].legend()
# Visulaizing the test set result
x_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start=x_set[:, 0].min() - 1, stop=x_set[:, 0].max() + 1, step=0.01),
np.arange(start=x_set[:, 1].min() - 1, stop=x_set[:, 1].max() + 1, step=0.01))
axes[1].contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha=0.75, cmap=ListedColormap(['#87CEEB', '#90EE90']))
axes[1].set_xlim(X1.min(), X1.max())
axes[1].set_ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
axes[1].scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
c=ListedColormap(['#0000FF', '#2ca02c'])(i), label=j)
axes[1].set_title('K-NN Algorithm (Test set)')
axes[1].set_xlabel('Age')
axes[1].set_ylabel('Estimated Salary')
axes[1].legend()
plt.tight_layout()
plt.show()
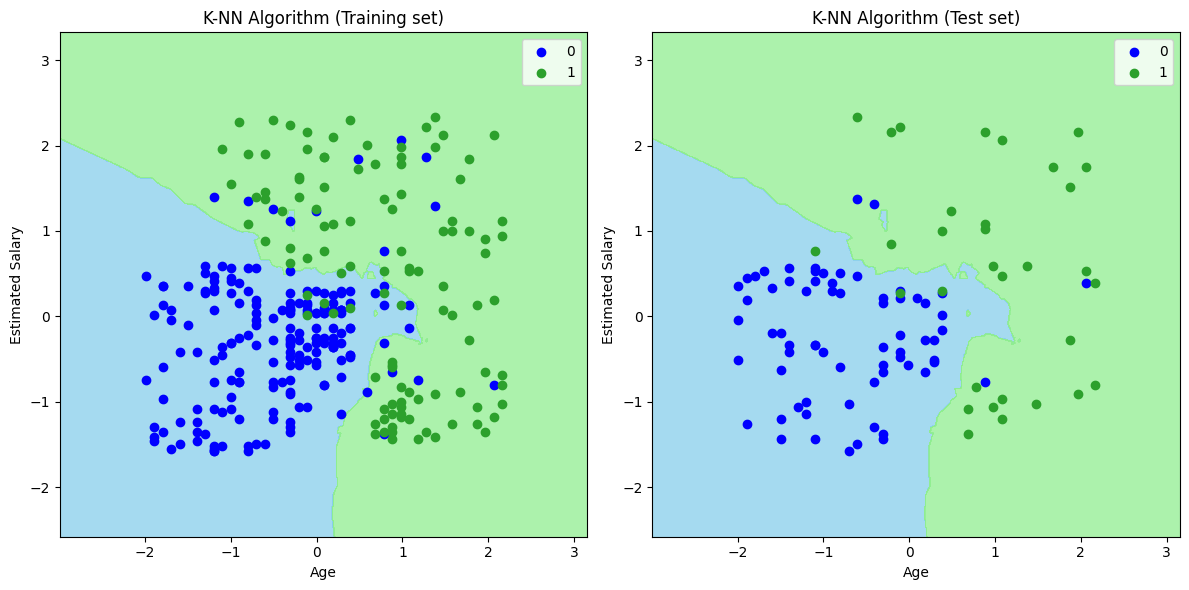
The output graph is different from the graph which we have occurred in Logistic Regression (For details, you can see Naive-Bayes classification.
Explanation for training dataset:
- As we can see the graph is showing the blue point and green points. The green points are for Purchased(1) and blue Points for not Purchased(0) variable.
- The graph is showing an irregular boundary instead of showing any straight line or any curve because it is a K-NN algorithm, i.e., finding the nearest neighbor.
- The graph has classified users in the correct categories as most of the users who didn't buy the SUV are in the blue region and users who bought the SUV are in the green region.
- The graph is showing good result but still, there are some green points in the blue region and blue points in the green region. But this is no big issue as by doing this model is prevented from overfitting issues.
- Hence our model is well trained.
Explanation for the test dataset:
- On the right side of the plot, plot for test datset is shown.
- As we can see in the graph, the predicted output is well good as most of the b;ue points are in the lightblue region and most of the green points are in the lightgreen region.
- However, there are few green points in the lightblue region and a few blue points in the lightgreen region. So these are the incorrect observations that we have observed in the confusion matrix.
References
- Confusion matrix details.
- My github Repositories on Remote sensing Machine learning
- A Visual Introduction To Linear regression (Best reference for theory and visualization).
- Book on Regression model: Regression and Other Stories
- Book on Statistics: The Elements of Statistical Learning
- Naïve Bayes Classifier Algorithm, JAVAPoint.com
- https://www.colorado.edu/amath/sites/default/files/attached-files/ch12_0.pdf
- One of the best description on Linear regression.
Some other interesting things to know:
- Visit my website on For Data, Big Data, Data-modeling, Datawarehouse, SQL, cloud-compute.
- Visit my website on Data engineering