The Recombination and Reionization Epochs: A Deep Dive into Cosmic History
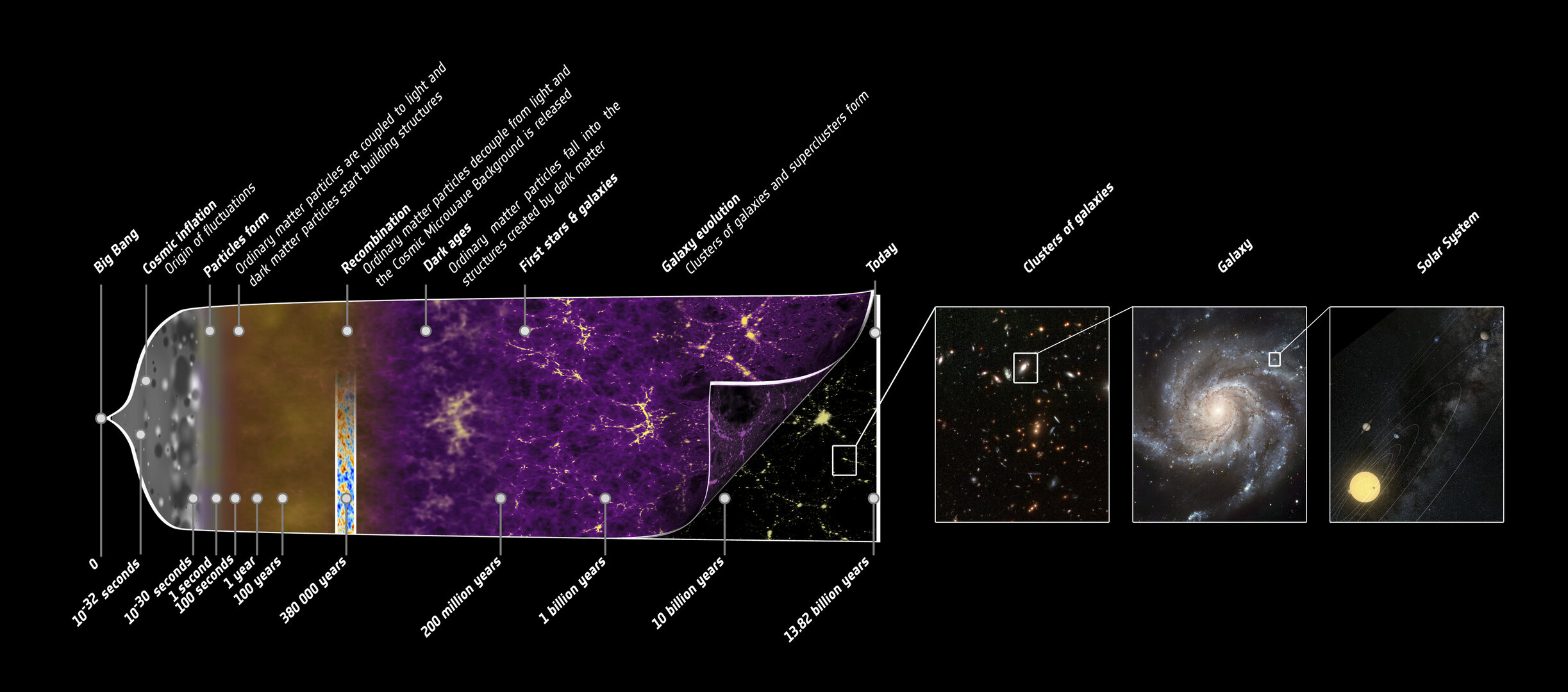
Before we dive into the specific epochs of Recombination and Reionization, it’s essential to understand the broader phases that the universe has gone through since its inception. The universe began as an incredibly hot, dense point and has expanded and cooled over billions of years, passing through various stages of transformation. Each of these stages was marked by significant physical phenomena, such as the formation of fundamental particles, the creation of atomic nuclei, and the birth of stars and galaxies.
From the earliest moments of the Planck Epoch, where the forces of nature were unified, to the Grand Unification Epoch and beyond, each period contributed to the universe's evolution. Cosmic inflation, the dominance of radiation, and the eventual emergence of matter and structure were key turning points that shaped the universe as we observe it today.
For the timline of our universe, please visit the page on Cosmic timeline of our universe.The Recombination Epoch
Immediately after the Big Bang, the Universe was extremely hot and dense. Under these conditions, atoms could not exist, and the matter was distributed as a highly ionised plasma. As the Universe expanded, however, its density and temperature dropped until (after about 380,000 years) the conditions were such that ions and electrons could 'recombine' to form atoms (mostly hydrogen and helium). This is known as the 'epoch of recombination'.We cannot actually observe the Universe before the epoch of recombination, since the ionised plasma that existed before this time was very efficient at scattering radiation. The result is that information about the early Universe (information astronomers detect in the form of photons) was not able to escape, hiding the early Universe from current observational strategies.
At the epoch of recombination, however, the ionised plasma gave way to neutral atoms, which did not scatter the photons but allowed them to travel freely. All photons emitted since this time have also been able to travel unimpeded, allowing astronomers to study objects all the way back to recombination. The oldest photons detected – those that were emitted at the epoch of recombination – make up the cosmic microwave radiation.
For more detail on the history of our universe, see my presentation:
If you would like to use any content from this presentation or its images, please contact me for permission at arunp77@gmail.com.
Key Events:
- Cooling of the Universe: As the universe expanded, it cooled from its initially hot and dense state. By the time of recombination, the temperature had dropped to around 3000 K.
- Formation of Neutral Atoms: The cooling allowed protons and electrons to combine and form neutral hydrogen atoms. This process is termed "recombination," although it's the first time these particles combined.
- Photon Decoupling: Before recombination, the universe was a hot, dense plasma where photons were constantly scattered by free electrons. The formation of neutral atoms allowed photons to travel freely, leading to the decoupling of matter and radiation. This event is what we observe today as the Cosmic Microwave Background (CMB) radiation.
Physics:
- Photon-Baryon Interaction: Prior to recombination, photons and baryons (protons and electrons) were tightly coupled through Thomson scattering. The decrease in free electrons reduced this scattering, enabling photons to decouple.
- Saha Equation: The recombination process is described by the Saha equation, which predicts the ionization state of hydrogen as the universe cooled.
The Saha equation describes the ionization state of a gas in thermal equilibrium. For hydrogen, it relates the ionization fraction to the temperature and density of the gas.
$$\frac{n_e n_p}{n_H} = \frac{g_e g_p}{g_H} \left( \frac{2 \pi m_e k_B T}{h^2} \right)^{3/2} e^{-E_i / k_B T}$$ Where:- \( n_e \) = number density of electrons
- \( n_p \) = number density of protons
- \( n_H \) = number density of hydrogen atoms
- \( g_e, g_p, g_H \) = statistical weights of electrons, protons, and hydrogen atoms, respectively
- \( m_e \) = mass of the electron
- \( k_B \) = Boltzmann constant
- \( T \) = temperature
- \( h \) = Planck constant
- \( E_i \) = ionization energy of hydrogen (13.6 eV)
Ionization Fraction ( \( x_e \) ): The ionization fraction \( x_e \) is defined as the ratio of free electrons to the total number of hydrogen nuclei.
$$x_e = \frac{n_e}{n_H + n_p}$$ Since \( n_p = n_e \) during recombination (quasi-neutrality), we have \( n_H = n_b - n_e \), where \( n_b \) is the total baryon number density.Matter and Radiation Densities: The baryon density can be related to the photon density \( n_\gamma \) by the baryon-to-photon ratio \( \eta \):
$$n_b = \eta n_\gamma$$ The photon number density is given by: $$n_\gamma = \frac{2 \zeta(3)}{\pi^2} \left( \frac{k_B T}{\hbar c} \right)^3$$ Where \( \zeta(3) \approx 1.202 \) is the Riemann zeta function of 3.Recombination Rate: The recombination rate \( \alpha(T) \) describes how quickly electrons and protons combine to form hydrogen atoms. It depends on temperature and is typically given by:
$$\alpha(T) = 4.309 \times 10^{-13} \left( \frac{T}{10^4 \text{ K}} \right)^{-0.6166} \left[ 1 + 0.6703 \left( \frac{T}{10^4 \text{ K}} \right)^{0.5300} \right] \text{ cm}^3 \text{s}^{-1}$$Differential Equation for Ionization Fraction:To find the evolution of the ionization fraction over time, we solve a differential equation that accounts for the balance between ionization and recombination rates:
$$\frac{dx_e}{dt} = -C \left[ \alpha(T) n_b x_e^2 - \beta(T) (1 - x_e) e^{-h\nu_{\alpha} / k_B T} \right]$$ Where:- \( \beta(T) \) is the photoionization rate,
- \( \nu_{\alpha} \) is the frequency of Lyman-alpha photons,
- \( C \) is the Peebles factor, which accounts for the fact that some recombinations directly to the ground state lead to the reionization of hydrogen.
- \( K \approx 7.19 \times 10^{-11} \text{ cm}^3 \text{s}^{-1} \)
- \( \Lambda \approx 8.22458 \text{ s}^{-1} \) is the two-photon decay rate of the 2s level of hydrogen
- \( n_H = n_b (1 - x_e) \) is the number density of neutral hydrogen.
Photoionization Rate: The photoionization rate \( \beta(T) \) is related to the recombination rate \( \alpha(T) \) by the Saha equilibrium at high temperatures:
$$\beta(T) = \alpha(T) \left( \frac{2 \pi m_e k_B T}{h^2} \right)^{3/2} e^{-E_i / k_B T}.$$ - Acoustic Oscillations: The interaction between photons and baryons before recombination led to acoustic oscillations in the primordial plasma. These oscillations left imprints on the CMB, observable as temperature fluctuations.
Complete set of equations:
To fully describe the recombination epoch, we need to consider a set of coupled differential equations that govern the evolution of the baryon temperature, the ionization fraction, and the expansion of the universe, including the effects of dark matter.- Ionization Fraction Equation: The ionization fraction \( x_e \) is governed by the following differential equation:
$$\frac{dx_e}{dz} = \frac{C}{H(z)(1+z)} \left[ \beta(T_b)(1 - x_e) e^{-h\nu_{\alpha} / k_B T_b} - \alpha(T_b) n_b x_e^2 \right]$$
Where:
- \( z \) is the redshift.
- \( C \) is the Peebles factor.
- \( H(z) \) is the Hubble parameter at redshift \( z \).
- \( T_b \) is the baryon temperature.
- \( \beta(T_b) \) is the photoionization rate.
- \( \alpha(T_b) \) is the recombination rate.
- \( n_b \) is the baryon number density.
- Peebles Factor \( C \):
The Peebles factor \( C \) accounts for the probability that a recombination event leads to a stable neutral hydrogen atom:
$$C = \frac{1 + K \Lambda n_H (1 - x_e)}{1 + K (\Lambda + \beta(T_b)) n_H (1 - x_e)}$$
where
- \( K \approx 7.19 \times 10^{-11} \text{ cm}^3 \text{s}^{-1} \).
- \( \Lambda \approx 8.22458 \text{ s}^{-1} \) is the two-photon decay rate of the hydrogen 2s level.
- \( n_H = n_b (1 - x_e) \) is the number density of neutral hydrogen.
- Recombination Rate \( \alpha(T_b) \): The recombination rate for hydrogen is temperature-dependent and can be approximated as: $$\alpha(T_b) = 4.309 \times 10^{-13} \left( \frac{T_b}{10^4 \text{ K}} \right)^{-0.6166} \left[ 1 + 0.6703 \left( \frac{T_b}{10^4 \text{ K}} \right)^{0.5300} \right] \text{ cm}^3 \text{s}^{-1}$$
- Photoionization Rate \( \beta(T_b) \): The photoionization rate is related to the recombination rate through: $$\beta(T_b) = \alpha(T_b) \left( \frac{2 \pi m_e k_B T_b}{h^2} \right)^{3/2} e^{-E_i / k_B T_b}.$$
- Baryon Temperature Equation: The evolution of the baryon temperature \( T_b \) is given by:
$$\frac{dT_b}{dz} = \frac{2 T_b}{1+z} - \frac{8 \sigma_T a_r T_{\gamma}^4}{3 m_e c H(z) (1+z)} \frac{x_e}{1+x_e+f_{\text{He}}} (T_b - T_{\gamma})$$
where:
- \( \sigma_T \) is the Thomson scattering cross-section.
- \( a_r \) is the radiation constant.
- \( T_{\gamma} \) is the temperature of the CMB.
- \( m_e \) is the electron mass.
- \( c \) is the speed of light.
- \( f_{\text{He}} \approx 0.08 \) is the helium fraction by number.
- Hubble Parameter \( H(z) \): The Hubble parameter at redshift \( z \) is given by:
$$H(z) = H_0 \sqrt{\Omega_m (1+z)^3 + \Omega_r (1+z)^4 + \Omega_\Lambda}$$
Where:
- \( H_0 \) is the present-day Hubble parameter.
- \( \Omega_m \), \( \Omega_r \), and \( \Omega_\Lambda \) are the density parameters for matter, radiation, and dark energy, respectively.
- Baryon Number Density \( n_b \): The baryon number density evolves with redshift as: $$n_b = n_{b0} (1+z)^3$$ Where \( n_{b0} \) is the present-day baryon number density.
- CMB Temperature \( T_{\gamma} \): The CMB temperature evolves with redshift as: $$T_{\gamma} = T_{\gamma 0} (1+z)$$ Where \( T_{\gamma 0} \approx 2.725 \text{ K} \) is the present-day CMB temperature.
- Putting It All Together: To study recombination in detail, one needs to solve these coupled differential equations numerically. The initial conditions are set at high redshift (typically \( z \sim 1500 \)) where the universe is fully ionized \( x_e \approx 1 \) and the baryon temperature \( T_b \approx T_{\gamma} \).
- Numerical Integration: The integration proceeds from high redshift to lower redshift, following these steps:
- Initialize the parameters: Set the initial conditions for \( x_e \), \( T_b \), and \( z \).
- Calculate the Hubble parameter \( H(z) \) using the given redshift \( z \).
- Evaluate the recombination rate \( \alpha(T_b) \) and photoionization rate \( \beta(T_b) \) at the current temperature \( T_b \).
- Compute the Peebles factor \( C \).
- Update the ionization fraction \( x_e \) using its differential equation.
- Update the baryon temperature \( T_b \) using its differential equation.
- Decrease the redshift \( z \) and repeat the steps until the desired redshift is reached.
The Reionization Epoch
The “Epoch of Reionization” is a period of the universe, when the first stars and galaxies were starting to form. Prior to this epoch, the universe was dark, suffused with a dense, obscuring fog of primordial gas. As the first stars switched on, their ultraviolet energy began to reionize the cosmos, punching ever-larger holes in their murky surroundings. Eventually, the effect of these young, massive stars and their infant galaxies enabled light to shine freely through space.Began around 150 million years after the Big Bang and lasted until about 1 billion years after the Big Bang.
Key Events:
- Formation of First Stars and Galaxies: The first sources of light, such as Population III stars, quasars, and early galaxies, formed and emitted high-energy ultraviolet (UV) photons.
- Ionization of Hydrogen: These UV photons reionized the neutral hydrogen in the intergalactic medium (IGM), converting it back into a plasma.
- Bubble Overlap: Ionized regions, or bubbles, created by individual sources of light began to overlap, leading to the gradual ionization of the entire IGM.
Physics:
- Ionization Fronts: High-energy photons from the first stars and galaxies created ionization fronts that propagated through the neutral hydrogen, ionizing it in the process.
- 21 cm Line: The neutral hydrogen before and during reionization can be studied through the 21 cm line, a specific radio wavelength emitted or absorbed by neutral hydrogen atoms.
- Feedback Mechanisms: Various feedback mechanisms, such as supernovae explosions and radiation pressure, influenced the rate and extent of reionization.
The Reionization Epoch: A Mathematical Perspective
The Reionization Epoch marks the period in the history of the universe during which the first sources of light, such as stars and quasars, reionized the previously neutral hydrogen in the intergalactic medium (IGM). This epoch began around 150 million years after the Big Bang and lasted until about 1 billion years after the Big Bang. Mathematically describing reionization involves understanding the interplay between radiation from the first luminous sources and the evolving state of the IGM. Here's a detailed mathematical treatment of the Reionization Epoch.- Ionization Fraction Evolution: The ionization fraction \( x_e \) represents the fraction of hydrogen that is ionized. The evolution of \( x_e \) can be described by the following differential equation:
$$\frac{dx_e}{dt} = \left( \frac{dx_e}{dt} \right)_{\text{ion}} - \left( \frac{dx_e}{dt} \right)_{\text{rec}}.$$
where:
- \( \left( \frac{dx_e}{dt} \right)_{\text{ion}} \) is the ionization rate per unit time.
- \( \left( \frac{dx_e}{dt} \right)_{\text{rec}} \) is the recombination rate per unit time.
- Ionization Rate: The ionization rate depends on the production rate of ionizing photons by the sources (stars, quasars) and the volume of the universe
$$\left( \frac{dx_e}{dt} \right)_{\text{ion}} = \frac{\dot{n}_{\gamma}}{n_H} f_{\text{esc}} (1 + \chi)$$
where:
- \( \dot{n}_{\gamma} \) is the rate of ionizing photons per unit volume.
- \( n_H \) is the number density of hydrogen atoms.
- \( f_{\text{esc}} \) is the escape fraction of ionizing photons from the sources into the IGM.
- \( \chi \approx 1 - \frac{n_{\text{He}}}{n_H} \) accounts for ionization of helium, with \( n_{\text{He}} \) being the number density of helium atoms.
- Recombination Rate: The recombination rate of ionized hydrogen is given by:
$$\left( \frac{dx_e}{dt} \right)_{\text{rec}} = - \alpha_B C n_H x_e^2$$
where:
- \( \alpha_B \) is the case B recombination coefficient, which depends on the temperature of the IGM.
- \( C \) is the clumping factor, accounting for the inhomogeneous distribution of matter in the IGM.
- Case B Recombination Coefficient: The case B recombination coefficient \( \alpha_B \) is given by: $$\alpha_B \approx 2.6 \times 10^{-13} \left( \frac{T}{10^4 \, \text{K}} \right)^{-0.7} \, \text{cm}^3 \text{s}^{-1}.$$ Where \( T \) is the temperature of the IGM.
- Clumping Factor \( C \): The clumping factor \( C \) quantifies the degree of inhomogeneity in the IGM: $$C = \frac{\langle n_H^2 \rangle}{\langle n_H \rangle^2}$$ Typically, \( C \) is estimated from simulations and observations and is of the order of 1-10 during reionization.
- Production Rate of Ionizing Photons: The production rate of ionizing photons per unit volume can be expressed as:
$$\dot{n}_{\gamma} = \rho_* \xi_{\text{ion}}$$
where:
- \( \rho_* \) is the star formation rate density.
- \( \xi_{\text{ion}} \) is the ionizing photon production efficiency, usually given in photons per second per solar mass of stars formed.
- Star Formation Rate Density \( \rho_* \): The star formation rate density evolves with redshift and can be parameterized using observational data or simulations. A common parameterization is: $$\rho_*(z) = \rho_0 \left( \frac{1+z}{1+z_0} \right)^\beta e^{-\gamma z}$$ Where \( \rho_0 \), \( z_0 \), \( \beta \), and \( \gamma \) are parameters fitted to observational data.
- Ionization Fraction Differential Equation: Combining the ionization and recombination rates, we get the differential equation for the ionization fraction \( x_e \): $$\frac{dx_e}{dt} = \frac{\rho_* \xi_{\text{ion}} f_{\text{esc}} (1 + \chi)}{n_H} - \alpha_B C n_H x_e^2$$ Converting to redshift \( z \) as the independent variable, using \( \frac{dz}{dt} = -H(z) (1+z) \), we obtain: $$\frac{dx_e}{dz} = -\frac{1}{H(z) (1+z)} \left[ \frac{\rho_* \xi_{\text{ion}} f_{\text{esc}} (1 + \chi)}{n_H} - \alpha_B C n_H x_e^2 \right]$$
- Hubble Parameter \( H(z) \): The Hubble parameter during the epoch of reionization is given by: $$H(z) = H_0 \sqrt{\Omega_m (1+z)^3 + \Omega_r (1+z)^4 + \Omega_\Lambda}$$ Where \( H_0 \) is the present-day Hubble constant, and \( \Omega_m \), \( \Omega_r \), and \( \Omega_\Lambda \) are the density parameters for matter, radiation, and dark energy, respectively.
Observational Evidence
- Cosmic Microwave Background (CMB): The CMB provides a snapshot of the universe at the time of recombination, with its tiny temperature fluctuations giving insights into the density variations of the early universe.
- Quasar Absorption Lines: Observations of distant quasars show absorption lines in their spectra due to neutral hydrogen, offering evidence of the IGM's ionization state at different epochs.
- 21 cm Cosmology: The 21 cm line from neutral hydrogen is a promising probe for studying the reionization epoch. Upcoming radio telescopes like the Square Kilometre Array (SKA) aim to map the distribution of neutral hydrogen and trace the reionization process.
Significance and Implications
- Structure Formation: The processes during recombination and reionization played crucial roles in the formation of large-scale structures, including galaxies, clusters, and cosmic filaments.
- Cosmic Timeline: Understanding these epochs helps refine the timeline of the universe's history, providing insights into the nature and formation of the first luminous objects.
- Fundamental Physics: These epochs serve as natural laboratories for studying fundamental physics, including the properties of dark matter, the nature of cosmic inflation, and the behavior of light and matter in the early universe.
Cosmic Microwave Background: A Mathematical Perspective
The Cosmic Microwave Background (CMB) is the relic radiation from the early universe, dating back to about 380,000 years after the Big Bang. At this time, the universe had cooled enough for electrons and protons to combine and form neutral hydrogen atoms, allowing photons to travel freely. This decoupling of matter and radiation is captured in the CMB. Mathematically, we can describe the CMB using several key concepts and equations.- Blackbody Spectrum of the CMB: The CMB is a nearly perfect blackbody radiation with a temperature of approximately 2.725 K. The spectral radiance \( B(\nu, T) \) of a blackbody at temperature \( T \) is given by Planck's law: $$B(\nu, T) = \frac{2 h \nu^3}{c^2} \frac{1}{e^{h\nu / k_B T} - 1}$$ where:
- \( \nu \) is the frequency of the radiation.
- \( h \) is Planck's constant.
- \( c \) is the speed of light.
- \( k_B \) is Boltzmann's constant.
- \( T \) is the temperature of the blackbody (2.725 K for the CMB).
- Temperature Anisotropies
The CMB is not perfectly uniform; it has small temperature anisotropies on the order of \( \Delta T / T \sim 10^{-5} \). These anisotropies are described using spherical harmonics \( Y_{\ell m}(\theta, \phi) \):
$$\frac{\Delta T}{T} (\theta, \phi) = \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} a_{\ell m} Y_{\ell m}(\theta, \phi).$$
where:
- \( \theta \) and \( \phi \) are the spherical coordinates.
- \( a_{\ell m} \) are the spherical harmonic coefficients.
- Power Spectrum: The statistical properties of the CMB anisotropies are encapsulated in the angular power spectrum \( C_\ell \): $$C_\ell = \langle |a_{\ell m}|^2 \rangle$$ The power spectrum provides information about the amplitude of temperature fluctuations at different angular scales (multipole moment \( \ell \)).
- Sachs-Wolfe Effect:
The temperature fluctuations in the CMB are partially caused by gravitational redshifts and blueshifts, described by the Sachs-Wolfe effect:
$$\left( \frac{\Delta T}{T} \right)_{\text{SW}} = \frac{1}{3} \Phi$$
where:
- \( \Phi \) is the gravitational potential perturbation.
- Acoustic Oscillations: The baryon-photon fluid in the early universe undergoes acoustic oscillations, leading to peaks and troughs in the power spectrum. The position of these peaks \( \ell \) can be related to the sound horizon \( r_s \) at recombination:
$$\ell \approx \frac{\pi D_A}{r_s}$$
where:
- \( D_A \) is the angular diameter distance to the surface of last scattering.
- \( r_s \) is the sound horizon at recombination, given by:
- \( c_s(t) \) is the sound speed in the early universe.
- \( a(t) \) is the scale factor.
- Boltzmann Equation for Photon Distribution: The evolution of the photon distribution function \( f_\gamma \) in the presence of anisotropies and inhomogeneities is governed by the Boltzmann equation:
$$\frac{\partial f_\gamma}{\partial t} + \frac{\partial f_\gamma}{\partial x^i} \frac{dx^i}{dt} + \frac{\partial f_\gamma}{\partial p^i} \frac{dp^i}{dt} = \left( \frac{\partial f_\gamma}{\partial t} \right)_{\text{coll}}.$$
where:
- \( f_\gamma \) is the photon distribution function.
- \( x^i \) are spatial coordinates.
- \( p^i \) are the components of the momentum vector.
- \( \left( \frac{\partial f_\gamma}{\partial t} \right)_{\text{coll}} \) is the collision term, accounting for interactions such as Compton scattering.
- Compton Scattering: Compton scattering between photons and electrons modifies the photon distribution. The collision term for Compton scattering is given by:
$$\left( \frac{\partial f_\gamma}{\partial t} \right)_{\text{coll}} = \sigma_T n_e \left( \frac{m_e}{p^0} \right) \left[ -\frac{T}{m_e} \frac{\partial f_\gamma}{\partial \ln p^0} \right]$$
where:
- \( \sigma_T \) is the Thomson scattering cross-section.
- \( n_e \) is the number density of electrons.
- \( m_e \) is the electron mass.
- \( p^0 \) is the energy of the photon.
- Polarization: The CMB is also polarized due to Thomson scattering. The polarization can be described using Stokes parameters \( Q \) and \( U \), and the polarization power spectra \( C_\ell^E \) and \( C_\ell^B \) for E-modes and B-modes, respectively: $$Q(\theta, \phi) = \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} a_{\ell m}^E Y_{\ell m}(\theta, \phi)$$ $$U(\theta, \phi) = \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} a_{\ell m}^B Y_{\ell m}(\theta, \phi)$$ Where \( a_{\ell m}^E \) and \( a_{\ell m}^B \) are the coefficients for E-mode and B-mode polarizations, respectively.
References
- Early star-forming galaxies and the reionization of the Universe, Brant E. Robertson et al. Nature 2010
- My notes on Monte Carlo simulation on my lecture note website.
- Gravitational Collapse A. Beesham & S. G. Ghosh
- Gravitational-collapse, W. B. BONNOR
- GitHub repo on gravitational collapse.
- Gravitational Collapse of Rotating Bodies Jeffrey M. Cohen
Some other interesting things to know:
- Visit my website on For Data, Big Data, Data-modeling, Datawarehouse, SQL, cloud-compute.
- Visit my website on Data engineering