Research

Gravitaional waves

Content

Introduction
Theoretical Background
Energy of Gravitational Waves and Quadrupole moments
Sources of Gravitational Waves
Gravitational Wave Sources During Cosmological Phase Transitions
Chiral Plasma and Gravitational Waves
Reference

Introduction to Gravitational Waves

Gravitational waves are ripples in spacetime that propagate as waves at the speed of light. They are produced by the acceleration of massive objects and carry energy away from their source. First predicted by Albert Einstein in 1916 as a consequence of his theory of General Relativity, these waves remained undetected for nearly a century until the landmark detection by the LIGO (Laser Interferometer Gravitational-Wave Observatory) collaboration in 2015.

Gravitational waves provide a unique way to observe astronomical phenomena that cannot be seen through electromagnetic radiation, such as black hole mergers, neutron star collisions, and possibly exotic early universe phenomena.

Basic Concept: Gravitational Waves in General Relativity

Gravitational waves are a key prediction of Einstein’s General Theory of Relativity. To understand the basic concept of gravitational waves, we must derive them mathematically as a solution to the linearized Einstein field equations. This section will develop the theory behind gravitational waves starting from Einstein's equations, focusing on the weak-field approximation and the wave-like nature of spacetime perturbations. Gravitational waves arise as a solution to the Einstein field equations in general relativity. These equations relate the curvature of spacetime (described by the Einstein tensor $ G_{\mu\nu} $) to the distribution of energy and momentum (encoded in the stress-energy tensor $ T_{\mu\nu} $): \[ G_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu} \]

Here $G_{\mu\nu}$ is a function of the metric $g_{\mu\nu}$ and its derivatives. $ T_{\mu\nu} $ represents the distribution of matter and energy. In the absence of matter (i.e., in vacuum), the equation reduces to:

$$G_{\mu\nu} = 0$$ This describes how spacetime is curved even in the absence of matter, a fundamental concept for gravitational waves.

Linearized Gravity

In many astrophysical scenarios, the curvature of spacetime is weak, and the metric $g_{\mu\nu}$ can be expressed as a small perturbation $h_{\mu\nu}$ on flat spacetime (the Minkowski metric $\eta_{\mu\nu}$): \[ g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}, \quad |h_{\mu\nu}| \ll 1 \] The metric perturbation $h_{\mu\nu}$ represents the deviation from flat spacetime. The Minkowski metric $\eta_{\mu\nu}$ in Cartesian coordinates is: $$\eta = \text{diag}(-1,+1,+1,+1)$$

Expansion of the Einstein Tensor

To derive the wave equation for gravitational waves, we must expand the Einstein tensor $G_{\mu\nu}$ to first order in $h_{\mu\nu}$. The Einstein tensor is related to the Ricci tensor $R_{\mu\nu}$ and the Ricci scalar $R$ via: \[ G_{\mu\nu} = R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R \] The Ricci tensor is obtained from the Christoffel symbols $ \Gamma^\lambda_{\mu\nu} $, which are functions of the metric and its first derivatives: \[ R_{\mu\nu} = \partial_\lambda \Gamma^\lambda_{\mu\nu} - \partial_\mu \Gamma^\lambda_{\lambda\nu} + \Gamma^\lambda_{\mu\nu} \Gamma^\sigma_{\lambda\sigma} - \Gamma^\sigma_{\mu\lambda} \Gamma^\lambda_{\nu\sigma} \] By linearizing these expressions, we find that the Einstein tensor to first order in $ h_{\mu\nu} $ is given by: \[ G_{\mu\nu}^{(1)} = \frac{1}{2} \left( \partial_\mu \partial_\nu h - \Box h_{\mu\nu} - \partial_\mu \partial^\lambda h_{\nu\lambda} - \partial_\nu \partial^\lambda h_{\mu\lambda} \right) \] where $ h = h^\lambda_\lambda $ is the trace of the perturbation, and $ \Box = \eta^{\mu\nu} \partial_\mu \partial_\nu $ is the d'Alembert operator.

Gauge Freedom and the Transverse-Traceless (TT) Gauge

Gravitational waves possess gauge freedom, meaning that different choices of coordinates lead to different representations of the same physical wave. By making a suitable coordinate transformation, we can simplify the form of $ h_{\mu\nu} $. A commonly used gauge is the Lorenz gauge, which imposes: \[ \partial^\mu h_{\mu\nu} = \frac{1}{2} \partial_\nu h \] However, a more useful gauge for gravitational waves is the transverse-traceless (TT) gauge, where we impose two conditions:

The perturbation is transverse: $ h_{0\mu} = 0 $ and $ h_{z\mu} = 0 $.
The perturbation is traceless: $ h^\mu_\mu = 0 $.

In the TT gauge, the linearized Einstein equations simplify, and the gravitational wave equation in vacuum becomes: \[ \Box h_{\mu\nu}^{\text{TT}} = 0 \] This is simply a wave equation, showing that $ h_{\mu\nu}^{\text{TT}} $ propagates as a wave through spacetime. The solutions to this equation are gravitational waves.

Solutions: Plane Waves

The simplest solutions to the wave equation $ \Box h_{\mu\nu}^{\text{TT}} = 0 $ are plane waves. A plane wave solution for gravitational waves can be written as: \[ h_{\mu\nu}^{\text{TT}}(t, \vec{x}) = A_{\mu\nu} \exp(i k_\alpha x^\alpha) + \text{c.c.} \] where $ A_{\mu\nu} $ is the amplitude tensor, $ k_\alpha $ is the wave vector, and $ x^\alpha = (t, \vec{x}) $ represents the spacetime coordinates. The wave vector satisfies the dispersion relation for massless waves: \[ k_\alpha k^\alpha = 0 \quad \Rightarrow \quad \omega = c |\vec{k}| \] Thus, gravitational waves propagate at the speed of light.

Polarization States

In the TT gauge, gravitational waves have only two independent components, which correspond to the two possible polarization states. These are conventionally denoted as $ h_+ $ and $ h_\times $. A gravitational wave propagating in the $ z $-direction can be written as: \[ h_{+}(t, z) = A_+ \cos(\omega t - k z), \quad h_{\times}(t, z) = A_\times \cos(\omega t - k z) \] These two polarization modes describe how the wave stretches and compresses spacetime in orthogonal directions. They represent the "plus" and "cross" polarizations of the wave. These two are transverse waves, meaning that the oscillations occur perpendicular to the direction of propagation. They have two polarizations, denoted as $ h_+ $ and $ h_\times $, which describe how they stretch and squeeze spacetime in orthogonal directions. The general form of the perturbation can be written as: \[ h_{\mu\nu}(t, \vec{x}) = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & h_+ & h_\times & 0 \\ 0 & h_\times & -h_+ & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \] These two polarization states correspond to different ways spacetime is deformed as the gravitational wave passes through a region. A gravitational wave traveling in the $ z $-direction can be expressed as a plane wave: \[ h_{\mu\nu}(t, z) = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & h_+(t - z/c) & h_\times(t - z/c) & 0 \\ 0 & h_\times(t - z/c) & -h_+(t - z/c) & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \] Here, the functions $ h_+(t - z/c) $ and $ h_\times(t - z/c) $ describe the two polarization modes of the gravitational wave as it propagates.

Therefore, GW represent ripples in spacetime that propagate as disturbances in the metric $ h_{\mu\nu} $. They arise from time-varying quadrupole moments of mass distributions and propagate at the speed of light. The weak-field approximation and the TT gauge simplify the Einstein field equations, revealing the wave-like nature of spacetime perturbations. Understanding the mathematical basis of gravitational waves not only deepens our understanding of General Relativity but also paves the way for exploring astrophysical phenomena through gravitational wave astronomy.

Energy of Gravitational Waves and Quadrupole moments

Energy of Gravitational Waves

Gravitational waves carry energy, which can be computed by evaluating the energy-momentum tensor for the perturbation. The effective energy density of gravitational waves is given by: \[ \rho_{\text{GW}} = \frac{1}{32 \pi G} \langle \dot{h}_{\mu\nu}^{\text{TT}} \dot{h}^{\mu\nu}_{\text{TT}} \rangle \] Here, the angle brackets $ \langle \dots \rangle $ denote an averaging over several wavelengths, and $ \dot{h}_{\mu\nu}^{\text{TT}} $ is the time derivative of the TT component of the perturbation. The energy flux of gravitational waves is proportional to $ \rho_{\text{GW}} $, and the total power radiated by a source is proportional to the quadrupole moment of the mass distribution (as discussed in earlier sections).

Quadrupole Moments

Gravitational waves are generated by the time-varying quadrupole moment of a mass distribution. This is in contrast to electromagnetic waves, which are generated by dipole moments. The quadrupole moment tensor $ Q_{ij} $ for a system of masses is given by: \[ Q_{ij} = \int \rho(x_i x_j - \frac{1}{3} \delta_{ij} r^2) d^3 x \] The rate of change of this quadrupole moment determines the amplitude of the emitted gravitational waves. The quadrupole radiation formula for the power radiated as gravitational waves is: \[ P_{\text{GW}} = \frac{G}{5c^5} \left\langle \dddot{Q}_{ij} \dddot{Q}^{ij} \right\rangle \] where $ \dddot{Q}_{ij} $ denotes the third time derivative of the quadrupole moment tensor. This formula shows that systems with large time-varying quadrupole moments (such as binary stars or black hole mergers) are strong emitters of gravitational waves.

Example: Binary Systems

The classic example of gravitational wave emission is a binary system, such as two compact objects (black holes or neutron stars) orbiting each other. The quadrupole moment of such a system is time-dependent due to the orbital motion, leading to the emission of gravitational waves. The energy carried away by these waves causes the orbit to decay, eventually leading to a merger. The loss of orbital energy due to gravitational radiation leads to the inspiral of the two objects, which is described by the Peters-Mathews equation: \[ \frac{dE}{dt} = -\frac{32 G^4}{5c^5} \frac{(M_1 M_2)^2 (M_1 + M_2)}{a^5} \] where $ M_1 $ and $ M_2 $ are the masses of the objects, and $ a $ is the orbital separation. This gradual inspiral produces a characteristic "chirp" signal, which was first observed by LIGO in the detection of merging black holes.

Sources of Gravitational Waves

Binary Systems: One of the primary sources of gravitational waves is binary systems, where two massive objects (such as black holes or neutron stars) orbit each other. As they lose energy through gravitational radiation, the two objects spiral closer together, eventually merging in a dramatic event that releases a burst of gravitational waves.
The inspiral and merger of black holes or neutron stars can be described by solving the Post-Newtonian approximation of the Einstein equations. In the final stages of the merger, full numerical relativity is needed to simulate the dynamics and the gravitational wave signal.
Stellar Collapse (Supernovae): Core-collapse supernovae, where a massive star undergoes gravitational collapse, can generate gravitational waves. These waves are generated when there is a significant asymmetry in the collapse. However, these signals are typically weaker and harder to detect compared to binary mergers.
Early Universe Sources: Gravitational waves could also be generated in the early universe during events such as:
- cosmic inflation
- phase transitions
- cosmic strings
- ...so many models ....

These waves would form a stochastic gravitational wave background, which could provide insight into the conditions of the early universe.

Gravitational Wave Sources During Cosmological Phase Transitions

Cosmological phase transitions in the early universe are pivotal events that can generate a stochastic background of gravitational waves (GWs). These transitions involve changes in the vacuum state of a field as the universe cools, leading to phenomena such as bubble nucleation and collisions, which are potent sources of gravitational radiation. This section provides a detailed mathematical explanation of how gravitational waves are produced during these phase transitions.

Introduction to Cosmological Phase Transitions

In the early universe, phase transitions occur as a result of spontaneous symmetry breaking in fundamental interactions. Notable transitions include:

Grand Unified Theory (GUT) Phase Transition: Occurs at temperatures around $10^{16}$ GeV.
Electroweak Phase Transition:Occurs at temperatures around $100$ GeV.
Quantum Chromodynamics (QCD) Phase Transition Occurs at temperatures around $200$ MeV.

Phase transitions can be classified as:

First-Order Phase Transitions: Proceed via bubble nucleation and involve latent heat.
Second-Order (or Crossover) Phase Transitions: Proceed smoothly without latent heat.

First-order phase transitions are of particular interest for gravitational wave production due to the violent dynamics they entail.

Dynamics of First-Order Phase Transitions

During a first-order phase transition:

Supercooling: The universe cools below the critical temperature $ T_c $, remaining in a metastable (false vacuum) state.
Bubble Nucleation: Quantum tunneling or thermal fluctuations cause bubbles of the true vacuum to form within the false vacuum.
Bubble Expansion: Bubbles expand, driven by the difference in vacuum energy ($ \Delta V $) between the true and false vacua.
Bubble Collisions and Percolation: Expanding bubbles collide and merge, completing the transition to the true vacuum phase.

These processes create anisotropic stresses in the energy-momentum tensor, which source gravitational waves.

Gravitational Wave Generation Mechanisms

There are three main mechanisms for gravitational wave production during first-order phase transitions:

Collision of Bubble Walls
Sound Waves in the Bubble Plasma
Magnetohydrodynamic (MHD) Turbulence

Mathematical Framework

Bubble Nucleation Rate: The nucleation rate per unit volume is given by: \[ \Gamma(T) = A(T) e^{-S(T)} \] where:
- $ A(T) $: Determinant prefactor, typically $ \sim T^4 $.
- $ S(T) $: Euclidean action of the critical bubble.
For thermal transitions, $ S(T) $ is the three-dimensional action $ S_3(T) $ divided by the temperature: \[ \Gamma(T) = T^4 \left( \frac{S_3(T)}{2\pi T} \right)^{3/2} e^{-S_3(T)/T} \]
The Euclidean Action: The action $ S_3(T) $ is given by: \[ S_3(T) = 4\pi \int_0^{R} r^2 dr \left[ \frac{1}{2} \left( \frac{d\phi}{dr} \right)^2 + V(\phi, T) \right] \] where:
- $ \phi(r) $: Field profile of the bubble.
- $ V(\phi, T) $: Temperature-dependent effective potential.
The critical bubble solution minimizes $ S_3(T) $.
Bubble Wall Velocity: The wall velocity $ v_w $ depends on the balance between the driving force from the vacuum energy difference and the friction from the plasma: \[ F_{\text{drive}} = \Delta V, \quad F_{\text{friction}} = \eta v_w \] Where $ \eta $ is the friction coefficient. The wall reaches a terminal velocity when $ F_{\text{drive}} = F_{\text{friction}} $.

Gravitational Waves from Bubble Collisions

The energy-momentum tensor for the scalar field $ \phi $ driving the transition is: \[ T_{\mu\nu} = \partial_\mu \phi \partial_\nu \phi - g_{\mu\nu} \left[ \frac{1}{2} \partial^\lambda \phi \partial_\lambda \phi - V(\phi) \right] \] Anisotropies in $ T_{\mu\nu} $ during bubble collisions source gravitational waves.

In the transverse-traceless (TT) gauge, the metric perturbation $ h_{ij} $ satisfies:

\[ \Box h_{ij}(\mathbf{x}, t) = 16\pi G T_{ij}^{\text{TT}}(\mathbf{x}, t) \] where

$ \Box $: D'Alembert operator.
$ T_{ij}^{\text{TT}} $: Transverse-traceless part of the energy-momentum tensor.

Solution for Gravitational Wave Energy Density

The energy density of gravitational waves is: \[ \rho_{\text{GW}} = \frac{\langle \dot{h}_{ij} \dot{h}_{ij} \rangle}{32\pi G} \] Where $ \langle \cdot \rangle $ denotes an average over several wavelengths.

Envelope Approximation

Assuming that the scalar field stress-energy is significant only at the bubble walls and neglecting overlaps, the gravitational wave spectrum can be calculated using the envelope approximation. The fractional energy density today is: \[ \Omega_{\text{GW},0} h^2 = \Omega_{\text{rad},0} h^2 \left( \frac{g_{*0}}{g_{*}} \right)^{1/3} \frac{\rho_{\text{GW}}}{\rho_{\text{rad}}} \] where

$ \Omega_{\text{rad},0} h^2 $: Present radiation density parameter.
$ g_{*0} $ and $ g_{*} $: Effective degrees of freedom today and at the time of the phase transition.

Gravitational Waves from Sound Waves

After bubble collisions, the kinetic energy of the plasma contributes to gravitational wave production.

The fluid velocity $ v(\mathbf{x}, t) $ generated by the expanding bubbles can be decomposed into solenoidal (vortical) and irrotational components.

The kinetic energy density is:

\[ \rho_{\text{kin}} = \frac{1}{2} w v^2 \] where

$ w $: Enthalpy density of the plasma.

The anisotropic stress tensor from the fluid is: \[ \Pi_{ij} = w \left( v_i v_j - \frac{1}{3} \delta_{ij} v^2 \right) \] This sources gravitational waves via: \[ \Box h_{ij}(\mathbf{x}, t) = \frac{16\pi G}{c^4} \Pi_{ij}(\mathbf{x}, t) \]

Power spectrum

The power spectrum of gravitational waves from sound waves is given by integrating over the Fourier transforms of $ \Pi_{ij} $: \[ P_h(k, t) = \frac{32\pi G}{c^4 k^2} \int d^3 k' \Pi_{ij}(\mathbf{k}', t) \Pi^{*}_{ij}(\mathbf{k} - \mathbf{k}', t) \]

Gravitational Waves from MHD Turbulence

The MHD turbulence generated by the bubble collisions also produces gravitational waves. Assuming Kolmogorov turbulence, the energy spectrum $ E(k) $ scales as: \[ E(k) \propto k^{-5/3} \] Between the injection scale $ k_{\text{inj}} $ and the dissipation scale $ k_{\text{diss}} $.

The gravitational wave energy density from turbulence is:

\[ \rho_{\text{GW}} \propto G \int_{k_{\text{min}}}^{k_{\text{max}}} dk \, k^2 \left| \tilde{v}(k) \right|^2 \] Where $ \tilde{v}(k) $ is the Fourier transform of the velocity field.

Spectral Shapes and Peak Frequencies

Bubble Collisions

The spectral shape from bubble collisions is generally a broken power law, with a peak frequency determined by: \[ f_{\text{coll}} = \frac{0.62}{1.8 - 0.1 v_w + v_w^2} \frac{\beta}{H_*} \frac{T_*}{100 \, \text{GeV}} \times 10^{-5} \, \text{Hz} \] where:

$ H_* $: Hubble parameter at the transition temperature $ T_* $.

Sound Waves

Peak frequency for sound waves: \[ f_{\text{sw}} = \frac{2}{\sqrt{3} v_w} \frac{\beta}{H_*} \frac{T_*}{100 \, \text{GeV}} \times 10^{-5} \, \text{Hz} \]

Turbulence

Peak frequency for turbulence is similar to that of sound waves.

Parameters Affecting Gravitational Wave Signals

Strength Parameter ($ \alpha $): Ratio of vacuum energy density to radiation energy density.
Inverse Duration Parameter ($ \beta $): Characterizes the timescale of the transition.
Wall Velocity ($ v_w $): Influences the efficiency of gravitational wave production.
Efficiency Factors ($ \kappa $): Determine how much vacuum energy goes into bulk motions.

Detectability with Gravitational Wave Observatories

Space-based detectors like LISA, or from NanoGrav, and BBO are designed to detect gravitational waves in the frequency range relevant for cosmological phase transitions. The signal-to-noise ratio (SNR) for detection depends on the sensitivity curve of the detector $ S_n(f) $ and the gravitational wave spectrum $ \Omega_{\text{GW}}(f) $: \[ \text{SNR} = \sqrt{ \int_{f_{\text{min}}}^{f_{\text{max}}} \left( \frac{h^2 \Omega_{\text{GW}}(f)}{h^2 \Omega_{\text{noise}}(f)} \right)^2 df } \]

Example calculation

Suppose we have a strong first-order phase transition with:

$ \alpha = 0.1 $
$ \beta/H_* = 100 $
$ v_w = 0.95 $
$ T_* = 100 \, \text{GeV} $
$ g_* = 100 $

Calculating the peak frequency for sound waves: \[ f_{\text{sw}} = \frac{2}{\sqrt{3} \times 0.95} \times \frac{100}{100} \times \frac{100}{100} \times 10^{-5} \, \text{Hz} \approx 1.2 \times 10^{-4} \, \text{Hz} \] Estimating the gravitational wave energy density: \[ \Omega_{\text{GW}} h^2 \approx 2.65 \times 10^{-6} \times \left( \frac{H_*}{\beta} \right) \left( \frac{\kappa_v \alpha}{1 + \alpha} \right)^2 v_w \] Assuming $ \kappa_v \approx 0.05 $: \[ \Omega_{\text{GW}} h^2 \approx 2.65 \times 10^{-6} \times \frac{1}{100} \left( \frac{0.05 \times 0.1}{1 + 0.1} \right)^2 \times 0.95 \approx 5 \times 10^{-11} \] This signal could be detectable by LISA, depending on the exact sensitivity and background noise.

Implications for Particle Physics and Cosmology

Probing New Physics: Gravitational waves from phase transitions can test models beyond the Standard Model, such as supersymmetry or extra dimensions.
Baryogenesis: First-order phase transitions are essential for electroweak baryogenesis mechanisms.
Dark Matter: Some dark matter models predict phase transitions that could produce observable gravitational waves.

Current Research and Challenges

Non-Perturbative Effects: Calculations of $ \kappa $ and $ \beta $ require non-perturbative methods like lattice simulations.
Bubble Wall Dynamics: Understanding wall velocities and interactions with the plasma is complex.
Overlap of Sources: Combining contributions from bubble collisions, sound waves, and turbulence requires careful modeling.

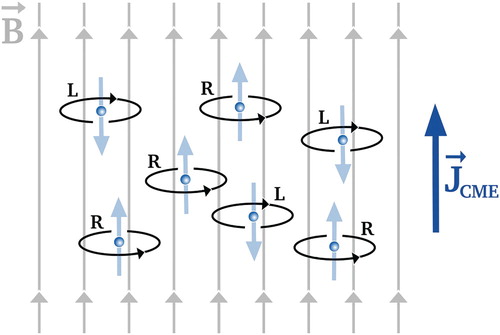
Gravitational waves from cosmological phase transitions offer a promising avenue to explore the early universe and fundamental physics. The mathematical modeling involves intricate calculations of bubble dynamics, plasma interactions, and gravitational wave propagation. Advances in detector technology and theoretical understanding may soon allow us to detect these signals, opening a new window into high-energy physics.

Chiral Plasma and Gravitational Waves

In my research, I explored the interaction between chiral plasma and gravitational waves. Chiral plasma in the early universe can generate anisotropic stresses that source gravitational waves.

Tensor Perturbations and Gravitational Waves

In the presence of chiral plasma, the energy-momentum tensor $ T_{\mu\nu} $ is no longer isotropic, and this can source tensor perturbations in the spacetime metric. These tensor perturbations behave as gravitational waves. The equation governing gravitational wave production is derived from the Einstein field equations with anisotropic stress: \[ \ddot{h}_{ij} + 3H \dot{h}_{ij} - \frac{1}{a^2} \nabla^2 h_{ij} = 16 \pi G \Pi_{ij} \] where $ h_{ij} $ is the tensor perturbation, $ H $ is the Hubble parameter, $ a $ is the scale factor, and $ \Pi_{ij} $ is the anisotropic stress due to the chiral plasma. These waves can propagate through the universe and contribute to the stochastic gravitational wave background.

Chiral Magnetic Instabilities and Gravitational Waves

In my research work, we found that the interaction between magnetic fields and chiral currents (via the chiral magnetic effect) generates gravitational waves. These waves can be produced by chiral plasma instabilities, which induce anisotropic stresses in the early universe plasma. The characteristic frequency of these gravitational waves depends on the scale of the magnetic field and the strength of the chiral imbalance. The power spectrum of these waves can be estimated from the dynamics of the chiral plasma.

Notes: Will write in details about the generation in a chiral plasma soon....

Detection of Gravitational Waves

Gravitational waves are detected by measuring the tiny distortions they produce in spacetime as they pass through a detector. The most famous detection method is based on laser interferometry, as used by LIGO and Virgo.

Interferometric Detection

An interferometer consists of two perpendicular arms along which laser beams are sent. When a gravitational wave passes through, it causes the length of the arms to oscillate, producing an interference pattern in the laser beams. The strain $ h $ produced by the gravitational wave is detected as a change in the interference pattern.

Current Detectors and Future Missions

LIGO and Virgo: These ground-based detectors have already detected several black hole and neutron star mergers. They operate in the frequency range of tens to thousands of Hertz, which is suitable for binary mergers.
LISA (Laser Interferometer Space Antenna): This future space-based observatory will detect gravitational waves in the millihertz frequency range, ideal for observing supermassive black hole mergers and early universe sources.
Pulsar Timing Arrays: These arrays measure the timing of pulsars and look for the influence of gravitational waves on the arrival times of their pulses. This technique is sensitive to very low-frequency

References

Chiral Plasma Instability and Primordial Gravitational waves, Sampurn Anad, Jitesh R. Bhatt & Arun Kumar Pandey [arXiv:1801.00650 [astro-ph.CO] (2019)] Eur. Phys. J. C (2019) 79: 119.
Gravitational waves in neutrino plasma and NANOGrav signal, Arun Kumar Pandey arXiv:2011.05821 [astro-ph.CO] (2020) [Eur.Phys.J.C 81 (2021) 5, 399]
Gravitational Waves and the Effort to Detect them, By Peter Shawhan

Some other interesting things to know:

Visit my website on For Data, Big Data, Data-modeling, Datawarehouse, SQL, cloud-compute.
Visit my website on Data engineering