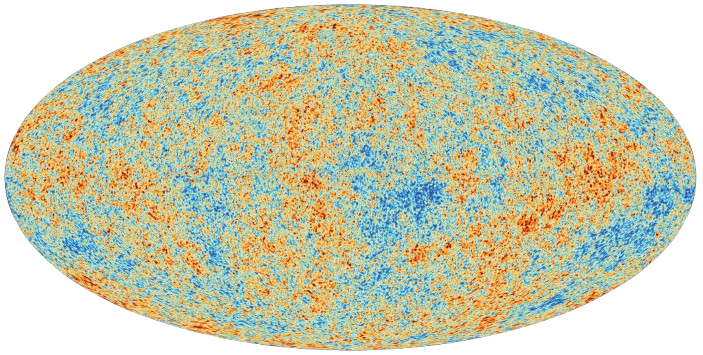
Cosmic Microwave Background (CMB)

Cosmic Microwave Background (CMB) radiation, copyright - ©ESA.

Content

  1. Introduction
  2. Background: FLRW Metric
  3. Covariant Form of Maxwell's Equations
  4. Electromagnetic Field Tensor in FLRW Metric
  5. Evolution of Magnetic Fields
  6. Magnetic Field Constraints
  7. Homogeneous Maxwell Equations in an Expanding Universe
  8. Inhomogeneous Maxwell Equations in an Expanding Universe
  9. Derivation of Maxwell's equation in expanding background
  10. Reference

Introduction

The Cosmic Microwave Background (CMB) is one of the most crucial discoveries in cosmology, offering us a direct glimpse into the infant universe. It is the afterglow radiation from the Big Bang, a relic that has traveled for over 13.8 billion years. The CMB provides valuable insight into the universe's composition, its geometry, and the processes that shaped the cosmos as we observe it today. This article delves into the physics, history, and significance of the CMB in cosmology.

What is the CMB?

The CMB is the oldest electromagnetic radiation in the universe. It was emitted about 380,000 years after the Big Bang during a time known as recombination. Before this epoch, the universe was a hot, dense plasma composed primarily of protons, electrons, and photons. Photons were continually interacting with the free electrons, making the universe opaque. However, as the universe expanded and cooled, protons and electrons combined to form neutral hydrogen atoms, reducing photon scattering. At this point, light could travel freely through space, marking the origin of the CMB.

The CMB is now observed as microwave radiation because its wavelength has stretched due to the expansion of the universe. It currently has a temperature of about 2.725 K (close to absolute zero) and appears almost uniform in all directions, with tiny fluctuations on the order of a few microkelvins.

Discovery of the CMB

The CMB was predicted by Ralph Alpher and Robert Herman in 1948 as a remnant of the Big Bang. However, its discovery came in 1965 when Arno Penzias and Robert Wilson, while working at Bell Labs, accidentally detected this faint microwave radiation. They found an excess noise in their radio telescope, which was isotropic and uniform, regardless of the telescope's orientation. This unexpected finding was soon recognized as the CMB, earning Penzias and Wilson the 1978 Nobel Prize in Physics.

The Physics of the CMB

The CMB provides a snapshot of the universe at a time when it transitioned from an opaque plasma to a transparent state. Its properties encode a wealth of information about the universe’s contents, expansion, and the conditions present in the early universe.
  1. Blackbody Radiation: The CMB is almost a perfect blackbody spectrum, meaning it follows the Planck distribution of radiation for a given temperature. The nearly perfect blackbody nature of the CMB provides strong evidence that the early universe was in thermal equilibrium.

    The spectrum of the CMB follows the equation for blackbody radiation:

    \[ I(\nu, T) = \frac{2h\nu^3}{c^2} \frac{1}{e^{h\nu/kT} - 1} \] where \( \nu \) is the frequency, \( T \) is the temperature, \( h \) is Planck’s constant, \( c \) is the speed of light, and \( k \) is Boltzmann's constant. The CMB spectrum matches this blackbody radiation curve precisely, peaking in the microwave range around 160.2 GHz, corresponding to a temperature of about 2.725 K.
  2. Temperature Fluctuations and Anisotropies: While the CMB is remarkably uniform, it contains tiny fluctuations in temperature, known as anisotropies. These small variations, on the order of one part in 100,000, are crucial because they provide a fossilized imprint of the density variations in the early universe. These density fluctuations would later grow under gravity to form galaxies, clusters, and large-scale structures in the universe.
  3. Polarization: In addition to temperature variations, the CMB is also polarized. As the photons scattered off electrons during the recombination epoch, the quadrupolar temperature fluctuations induced polarization. This polarization can be decomposed into E-modes and B-modes. The E-modes are related to the density fluctuations, while the B-modes could contain signatures of gravitational waves from the early universe, possibly from inflation

Cosmological Implications of the CMB

The CMB is a cornerstone in modern cosmology, offering insights into the universe’s composition, geometry, and age. The detailed analysis of the CMB has led to the development of the Lambda Cold Dark Matter (ΛCDM) model, the standard model of cosmology.
  1. Flatness and Geometry of the Universe: Measurements of the CMB's angular power spectrum provide strong evidence that the universe is spatially flat. This implies that the sum of the density parameters (matter, dark matter, and dark energy) is very close to 1. The curvature parameter, \( \Omega_k \), is found to be consistent with zero, implying a flat geometry.
  2. Baryon Acoustic Oscillations: The CMB also contains signatures of baryon acoustic oscillations (BAO), which are the regular, periodic fluctuations in the density of the visible baryonic matter of the universe. These oscillations arose due to the interplay between pressure from photon-baryon interactions and the gravitational pull from dark matter. The characteristic scale of BAOs, visible as a peak in the CMB power spectrum, is used as a "standard ruler" to measure distances in the universe.
  3. Dark Matter and Dark Energy: The CMB’s anisotropies provide compelling evidence for dark matter and dark energy. The ΛCDM model indicates that the universe is composed of approximately 5% ordinary matter, 27% dark matter, and 68% dark energy. The detailed pattern of anisotropies cannot be explained without invoking cold dark matter and the repulsive force of dark energy driving the accelerated expansion of the universe.
  4. Primordial Inflation: The uniformity of the CMB across vast regions of the sky suggests that the universe underwent a brief period of rapid expansion known as inflation. Inflation solves several puzzles in cosmology, including the horizon problem (why regions of the universe separated by vast distances have nearly the same temperature) and the flatness problem (why the universe appears flat). While the detailed mechanism of inflation is still under investigation, the CMB provides key evidence supporting its occurrence.

Major CMB Experiments and Results

Over the decades, numerous missions and experiments have been conducted to study the CMB, with progressively greater precision.
  1. COBE (Cosmic Background Explorer): Launched in 1989, the COBE satellite was the first to measure the CMB’s blackbody spectrum and detect large-scale anisotropies. It confirmed that the CMB is a nearly perfect blackbody and provided the first detection of temperature fluctuations, leading to a Nobel Prize for John Mather and George Smoot.
  2. WMAP (Wilkinson Microwave Anisotropy Probe): Launched in 2001, WMAP provided a much more detailed map of the CMB anisotropies. It measured the universe’s age, geometry, and composition with unprecedented precision. WMAP confirmed that the universe is about 13.8 billion years old, flat, and dominated by dark energy.
  3. Planck Satellite: The European Space Agency's Planck satellite, launched in 2009, is the most precise CMB experiment to date. It has mapped the anisotropies of the CMB with greater detail and sensitivity, further refining our understanding of cosmological parameters. Planck’s results have provided strong evidence for the ΛCDM model, placing tight constraints on the amount of dark matter and dark energy.

Future Prospects: The CMB and Beyond

While current observations of the CMB have provided a deep understanding of the universe's history and composition, several open questions remain, such as the exact nature of dark matter, dark energy, and the physics of inflation. Future CMB experiments aim to detect the primordial B-modes—a potential signal of gravitational waves generated during inflation. The detection of these B-modes would be a significant breakthrough in understanding the very early universe and the physics of inflation.

Upcoming missions like the LiteBIRD satellite and CMB-S4 ground-based observatories aim to further investigate the polarization of the CMB and search for these elusive signals.

Temperature Anisotropies in the CMB

The temperature anisotropies in the CMB represent small fluctuations in the temperature of the radiation across the sky. These fluctuations, on the order of one part in 100,000, are essential for understanding the large-scale structure of the universe, as they encode information about the early universe, including its composition, geometry, and the physics of inflation.

In this section, we'll derive the formalism for temperature anisotropies in the CMB from scratch, starting from the physical origins of these fluctuations to the mathematical description.

Physical Origin of Temperature Anisotropies
The temperature anisotropies in the CMB arise from several key physical mechanisms that occurred in the early universe:
  • Density fluctuations: At the time of recombination (~380,000 years after the Big Bang), the universe had small variations in density. Regions with slightly higher densities had stronger gravitational potentials, affecting the temperature of the photons escaping from those regions.
  • Gravitational redshift (Sachs-Wolfe effect): The Sachs-Wolfe effect is one of the dominant sources of temperature anisotropies on large angular scales (\( \ell \lesssim 100 \)). It is caused by the redshift of photons climbing out of gravitational potential wells at the time of last scattering. The temperature fluctuation due to this effect can be written as: \[ \frac{\Delta T}{T} \sim \frac{\delta \Phi}{c^2} \] where \( \delta \Phi \) is the gravitational potential perturbation.
  • Doppler effect: The motion of baryons (normal matter) at the time of recombination can induce Doppler shifts in the frequency of photons, leading to temperature fluctuations.
  • Acoustic oscillations: In the early universe, interactions between photons and baryons created pressure waves, or acoustic oscillations, in the photon-baryon plasma. Before recombination, these oscillations were driven by the competition between gravity and radiation pressure. As a result, they left distinct imprints on the temperature fluctuations of the Cosmic Microwave Background (CMB), producing a series of peaks in the CMB power spectrum, especially at smaller angular scales.
CMB temperature anisotropies : Mathematical explanantion
The CMB temperature anisotropies are small fluctuations around the mean temperature \( T_0 \approx 2.725 \, \text{K} \). It is described on the sky plane as a function \( \Delta T(\hat{n}) \), where \( \hat{n} \) is the direction on the sky and \( \Delta T(\hat{n}) = T(\hat{n}) - \bar{T} \) is the difference between the observed temperature in that direction and the average temperature \( \bar{T} = T_0 \) of the CMB. where:
  • \( \Delta T(\hat{n}) \) is the temperature fluctuation in the direction \( \hat{n} \).
  • \( T(\hat{n}) \) is the temperature observed in direction \( \hat{n} \).

Instead of analyzing these fluctuations in real space, we expand them in spherical harmonics, \( Y_{\ell m}(\hat{n}) \), since the CMB fluctuations occur on the surface of a sphere:

\[ \frac{\Delta T(\hat{n})}{\bar{T}} = \frac{T(\hat{n}) - T_0}{T_0} = \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} a_{\ell m} Y_{\ell m}(\hat{n}) \]

where:

  • \( \ell \) is the multipole moment corresponding to angular scales \( \theta \sim 180^\circ/\ell \).
  • \( m \) is the azimuthal quantum number (\( -\ell \leq m \leq \ell \)).
  • \( a_{\ell m} \) are the multipole coefficients representing the amplitude of fluctuations at each \( \ell \) and \( m \).

Two-Point Correlation Function and Statistical Isotropy

To statistically characterize the temperature anisotropies, we compute the two-point correlation function \( C(\theta) \), which measures how temperature fluctuations at two points on the sky, separated by an angle \( \theta \), are related: \[ C(\theta) = \left\langle \frac{\Delta T(\hat{n})}{T_0} \frac{\Delta T(\hat{n}')}{T_0} \right\rangle \] Assuming statistical isotropy, meaning the fluctuations are the same in every direction, \( C(\theta) \) depends only on the angular separation \( \theta \) between the two points and not their specific locations. Substituting the spherical harmonic expansion into the correlation function, we obtain: \[ C(\theta) = \sum_{\ell} \frac{2\ell + 1}{4\pi} C_\ell P_\ell(\cos\theta) \] Here, \( P_\ell(\cos\theta) \) are the

Legendre polynomials

, and \( C_\ell \) is the angular power spectrum. The power spectrum \( C_\ell \) represents the variance of the temperature fluctuations at a given angular scale.

Power Spectrum \( C_\ell \) and Angular Scales

The power spectrum \( C_\ell \) gives us a statistical description of the CMB anisotropies as a function of angular scale. The multipole \( \ell \) corresponds to different angular scales on the sky: \[ \theta \sim \frac{180^\circ}{\ell} \]
  • Low \( \ell \) values (small \( \ell \)) represent large angular scales on the sky.
  • High \( \ell \) values (large \( \ell \)) represent small angular scales.
The total variance of the temperature fluctuations is then given by summing over all multipoles: \[ \langle \left( \frac{\Delta T}{T} \right)^2 \rangle = \frac{1}{4\pi} \sum_{\ell=0}^{\infty} (2\ell + 1) C_{\ell} \] This equation shows how the power spectrum \( C_\ell \) distributes the temperature variance across different angular scales.
Statistical Properties of the Temperature Anisotropies:
  • The CMB temperature anisotropies are assumed to be a Gaussian random field, meaning that the fluctuations are statistically isotropic and homogeneous. As a result, the ensemble average of the multipole moments \( a_{\ell m} \) is zero:

    \[ \langle a_{\ell m} \rangle = 0 \] However, the variance of these moments is not zero and is expressed in terms of the power spectrum \( C_{\ell} \), which encodes the angular distribution of the temperature anisotropies: \[ \langle a_{\ell m} a_{\ell' m'}^* \rangle = C_{\ell} \delta_{\ell \ell'} \delta_{m m'} \] This equation shows that the variance of the \( a_{\ell m} \)'s depends only on \( \ell \), reflecting the fact that the temperature fluctuations are statistically isotropic. \[ \langle a_{\ell m} \rangle = 0 \]
  • Orthonormality of Spherical Harmonics: \[ \int Y_{\ell m}(\hat{n}) Y_{\ell' m'}^*(\hat{n}) \, d\Omega = \delta_{\ell \ell'} \delta_{m m'} \] where \( d\Omega = \sin\theta \, d\theta \, d\phi \), and \( \delta \) is the Kronecker delta.
  • Completeness: \[ \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} Y_{\ell m}(\hat{n}) Y_{\ell m}^*(\hat{n}') = \delta(\hat{n} - \hat{n}') \]

Derivation of the Power Spectrum \( C_\ell \)

The power spectrum \( C_{\ell} \) describes how much variance in the temperature fluctuations occurs at a given angular scale. To understand its physical meaning, we need to connect \( C_{\ell} \) with the temperature fluctuations.

To compute \( C_\ell \), we can use either the correlation function or the spherical harmonic coefficients \( a_{\ell m} \). The two approaches are related by the **addition theorem** of spherical harmonics:

\[ \sum_{m=-\ell}^{\ell} Y_{\ell m}(\hat{n}) Y_{\ell m}^*(\hat{n}') = \frac{2\ell + 1}{4\pi} P_\ell(\cos\theta) \] Thus, the correlation function \( C(\theta) \) can be expressed in terms of the power spectrum \( C_\ell \): \[ C(\theta) = \sum_{\ell} C_\ell \frac{2\ell + 1}{4\pi} P_\ell(\cos\theta) \] In practice, \( C_\ell \) can also be computed from the spherical harmonic coefficients as: \[ C_\ell = \frac{1}{2\ell + 1} \sum_{m=-\ell}^{\ell} |a_{\ell m}|^2 \] This provides a practical way to estimate \( C_\ell \) from observational data of the CMB.
Physical Interpretation of the Power Spectrum
The angular power spectrum \( C_\ell \) describes how temperature fluctuations in the CMB vary across different angular scales:
  • Low \( \ell \) (Large Angular Scales): These correspond to large-scale fluctuations, which capture information about the early universe's global geometry and the largest structures.
  • High \( \ell \) (Small Angular Scales): These correspond to smaller-scale fluctuations, including the detailed physics of sound waves (acoustic oscillations) in the photon-baryon plasma before recombination.

The acoustic peaks in the power spectrum reflect these oscillations, with the positions and heights of the peaks providing insights into the universe’s composition (e.g., dark matter, baryonic matter, dark energy) and curvature. The damping tail at very high \( \ell \) occurs due to photon diffusion, which smooths out small-scale fluctuations.

The angular power spectrum \( C_\ell \) is a crucial tool in cosmology, encapsulating the temperature fluctuations across different angular scales of the CMB. By expanding the temperature anisotropies in spherical harmonics, computing their correlations, and assuming statistical isotropy, we derive a robust framework for understanding the universe's early conditions, matter content, and geometry.

The detailed analysis of the power spectrum has allowed cosmologists to refine the standard ΛCDM model and has been instrumental in understanding the universe's expansion, the relative amounts of dark matter and dark energy, and the formation of large-scale structures.

References

Some other interesting things to know:

Portfolio section Content