Central Limit Theorem (CLT)
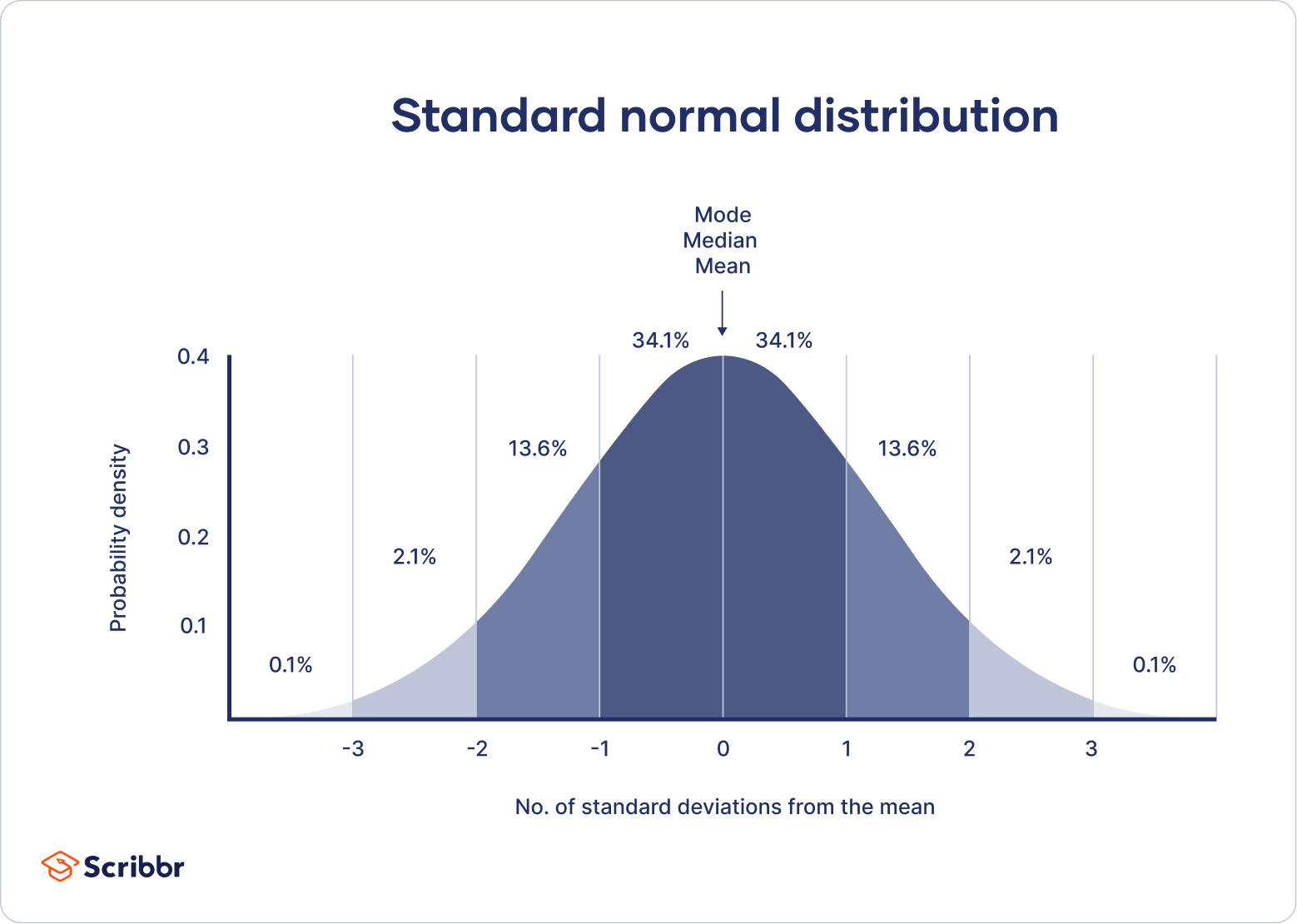
The Central Limit Theorem (CLT) is a fundamental concept in statistics and probability theory. It states that under certain conditions, the sampling distribution of the mean of a random sample drawn from any population will approximate a normal distribution, regardless of the shape of the original population distribution.
As the sample size n increases, the sampling distribution of the mean approaches a normal distribution with mean equal to the population mean and standard deviation equal to the population standard deviation divided by the square root of the sample size.
Conditions for the CLT
- Independence: Observations must be independent.
- Random sampling: Samples must be drawn randomly.
- Finite variance: The population must have finite variance.
The CLT allows us to make statistical inferences about population means and proportions using sample data. It is widely used in hypothesis testing, confidence intervals, and statistical modeling.
Applications of the CLT
- Estimating population parameters: Constructing confidence intervals for population means.
- Hypothesis testing: Testing assumptions about population parameters.
- Machine learning: Justifying normality assumptions in regression models.
Mathematical Formulation
Here, μ is the population mean, σ is the population standard deviation, and n is the sample size.
where z* is the critical value from the standard normal distribution. For a 95% confidence level, z* = 1.96.
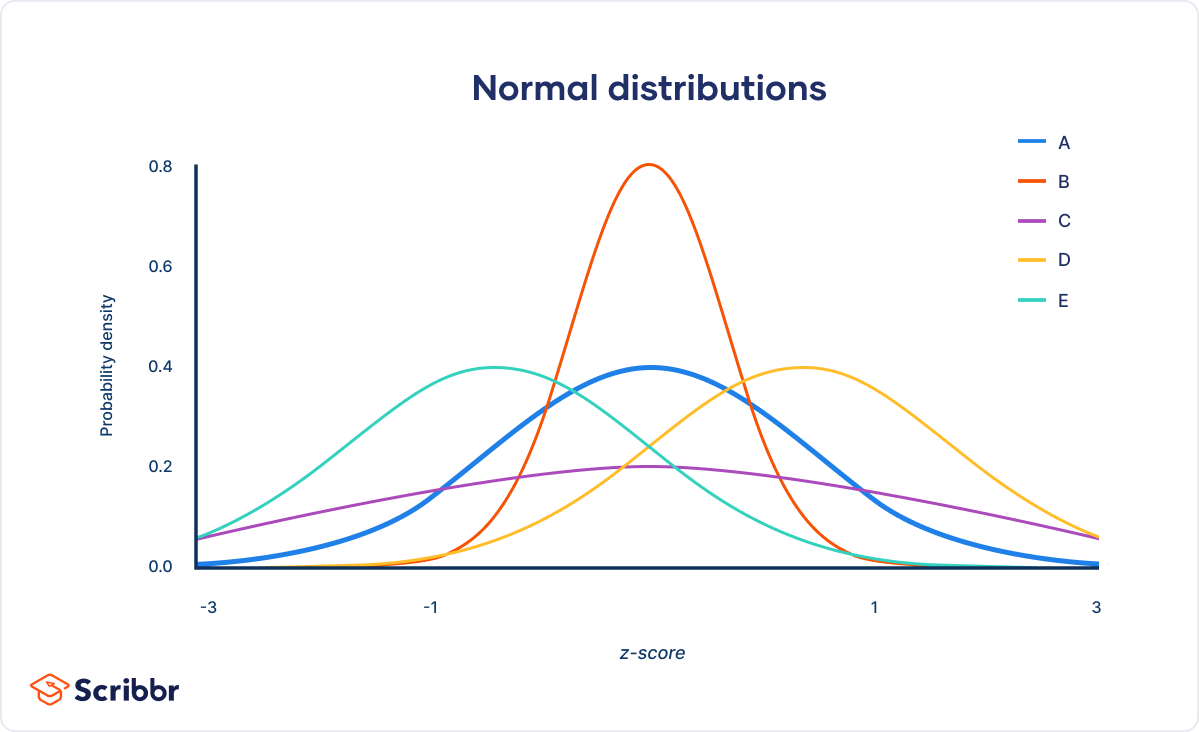
Normal vs Standard Normal Distribution
| Curve | Description |
|---|---|
| A (M = 0, SD = 1) | Standard normal distribution |
| B (M = 0, SD = 0.5) | Squeezed distribution |
| C (M = 0, SD = 2) | Stretched distribution |
| D (M = 1, SD = 1) | Shifted right |
| E (M = −1, SD = 1) | Shifted left |
Standardizing a Normal Distribution
- x — individual value
- μ — mean
- σ — standard deviation