Statistics ¶
Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It is a discipline that is used in many fields, including science, engineering, medicine, social sciences, and business.
The primary goal of statistics is to make inferences about a population based on a sample of data. This involves using various statistical methods and techniques to analyze the data and draw conclusions about the population.
Statistics is a broad field that has many sub-disciplines or branches. Here are some of the major branches of statistics:
Descriptive statistics: This branch of statistics deals with summarizing and describing data from a sample or population using measures such as mean, median, mode, variance, standard deviation, and correlation.
Inferential statistics: This branch of statistics deals with making inferences or predictions about a population based on a sample of data using statistical hypothesis testing, confidence intervals, and regression analysis.
Probability theory: This branch of statistics deals with the mathematical study of random events and the likelihood of their occurrence.
Biostatistics: This branch of statistics is concerned with the analysis and interpretation of data related to health and medicine.
Econometrics: This branch of statistics deals with the application of statistical methods to economic data to model and analyze economic relationships.
Psychometrics: This branch of statistics deals with the design and analysis of tests and questionnaires to measure psychological traits and abilities.
Spatial statistics: This branch of statistics deals with the analysis of geospatial data to understand patterns and relationships in geographic space.
Time series analysis: This branch of statistics deals with the analysis of data collected over time to identify trends, patterns, and seasonality.
Bayesian statistics: This branch of statistics deals with the use of Bayesian methods to analyze and interpret data, which involves updating prior knowledge or beliefs based on new data.
Machine learning: This branch of statistics deals with the development of algorithms and models that can learn and make predictions from data, including supervised and unsupervised learning techniques.
Statistics is used in a wide variety of applications, from determining the effectiveness of a new medical treatment to analyzing financial data to make investment decisions. It is an important tool for decision-making and problem-solving in many different fields.
Understanding statistics is important for researchers, data analysts, and decision-makers who need to analyze and interpret data to make informed decisions.# Statistics
Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It is a discipline that is used in many fields, including science, engineering, medicine, social sciences, and business.
The primary goal of statistics is to make inferences about a population based on a sample of data. This involves using various statistical methods and techniques to analyze the data and draw conclusions about the population.
Statistics is a broad field that has many sub-disciplines or branches. Here are some of the major branches of statistics:
Descriptive statistics: This branch of statistics deals with summarizing and describing data from a sample or population using measures such as mean, median, mode, variance, standard deviation, and correlation.
Inferential statistics: This branch of statistics deals with making inferences or predictions about a population based on a sample of data using statistical hypothesis testing, confidence intervals, and regression analysis.
Probability theory: This branch of statistics deals with the mathematical study of random events and the likelihood of their occurrence.
Biostatistics: This branch of statistics is concerned with the analysis and interpretation of data related to health and medicine.
Econometrics: This branch of statistics deals with the application of statistical methods to economic data to model and analyze economic relationships.
Psychometrics: This branch of statistics deals with the design and analysis of tests and questionnaires to measure psychological traits and abilities.
Spatial statistics: This branch of statistics deals with the analysis of geospatial data to understand patterns and relationships in geographic space.
Time series analysis: This branch of statistics deals with the analysis of data collected over time to identify trends, patterns, and seasonality.
Bayesian statistics: This branch of statistics deals with the use of Bayesian methods to analyze and interpret data, which involves updating prior knowledge or beliefs based on new data.
Machine learning: This branch of statistics deals with the development of algorithms and models that can learn and make predictions from data, including supervised and unsupervised learning techniques.
Statistics is used in a wide variety of applications, from determining the effectiveness of a new medical treatment to analyzing financial data to make investment decisions. It is an important tool for decision-making and problem-solving in many different fields.
Understanding statistics is important for researchers, data analysts, and decision-makers who need to analyze and interpret data to make informed decisions.
Population vs. Sample ¶
- A population is the entire group that you want to draw conclusions about.
- A sample is the specific group that you will collect data from. The size of the sample is always less than the total size of the population.
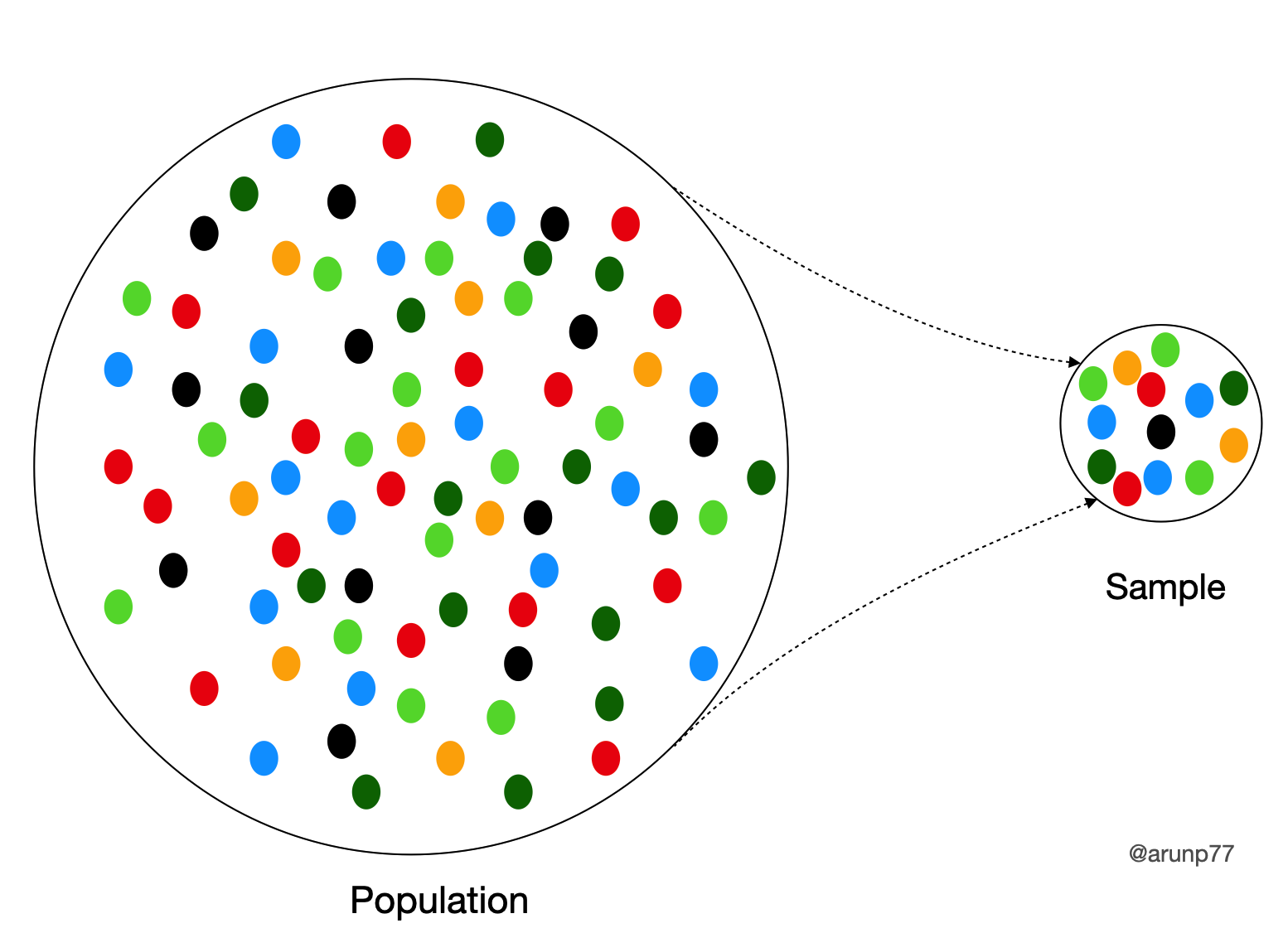
Example: let's say we are interested in studying the average height of all adults in a certain country. The population in this case would be all adults in that country, while a sample would be a group of randomly selected adults from that country who we actually measure and collect data on.
It's important to note that the characteristics of a population can be inferred from the characteristics of a sample, but this requires appropriate sampling techniques and statistical analysis.
| Population | Sample | |
|---|---|---|
| Definition | The entire group of individuals, objects, or events that we are interested in studying. | A subset of the population that we actually collect data on. |
| Size | Usually very large, can be infinite. | Smaller than the population, usually less than 10% of the population. |
| Selection | All members of the population are potentially included in the study. | Members of the population are selected to be included in the study. |
| Characteristics | Parameters of the population can be determined with complete accuracy. | Statistics of the sample can be used to make inferences about the parameters of the population. |
| Importance | The ultimate goal of statistical inference is to make accurate statements about the population. | The sample is used to estimate characteristics of the population when it is impractical or impossible to study the entire population. |
| Example | All dogs in a certain city. | A randomly selected group of 100 dogs from that city. |
Collecting data from a population and sample and Reasons for sampling¶
Collecting data from a population involves gathering information about every individual, object or event that belongs to the group of interest, which can be very time-consuming, expensive, and sometimes even impossible. That's why researchers often use sampling, which involves collecting data from a subset of the population that is representative of the entire population.
Sampling has several advantages, including:
- Efficiency: Collecting data from a sample is generally faster and less expensive than collecting data from the entire population.
- Feasibility: Sometimes it is impossible to study the entire population, so a sample provides a more practical way to study the population.
- Accuracy: If the sample is selected properly, the results can be just as accurate as if the entire population had been studied.
- Accessibility: Sampling is often the only way to study rare or inaccessible populations, such as endangered species, historical artifacts, or celestial bodies.
However, sampling also has some potential drawbacks, including:
- Sampling error: The results of a sample may differ from the true values of the population due to random variation in the selection process.
- Bias: The sample may not be representative of the population if certain groups are over- or under-represented in the sample.
- Cost: Depending on the sampling method, collecting a sample can still be costly and time-consuming.
To reduce the potential for bias and ensure that the sample is representative of the population, researchers often use random sampling techniques, such as simple random sampling, stratified sampling, cluster sampling, or systematic sampling. By selecting a sample that is representative of the population and collecting data in a systematic way, researchers can obtain accurate and reliable information about the population.
Population parameter vs. sample statistic¶
In statistics, we use population parameters and sample statistics to describe the characteristics of a population and a sample, respectively.
- population parameter: is a numerical value that describes a characteristic of the entire population. Examples of population parameters include the
- population mean,
- population standard deviation,
- population proportion, etc.
These parameters are usually unknown, and we use statistical inference techniques to estimate them from a sample.
Sample statistic: On the other hand, a sample statistic is a numerical value that describes a characteristic of a sample. Examples of sample statistics include the
- sample mean,
- sample standard deviation,
- sample proportion, etc.
These statistics are used to estimate the population parameters.
The key difference between population parameters and sample statistics is that population parameters are fixed values that describe the entire population, while sample statistics can vary from sample to sample and only describe the particular sample that was selected.
Example: 1 Suppose we are interested in studying the average height of all students in a school. The population parameter would be the true population mean height, which we cannot observe directly. To estimate this parameter, we would collect a sample of students and calculate the sample mean height. This sample mean height is the sample statistic, which can vary from sample to sample.
Example: 2 Another example is the proportion of voters who support a particular candidate in an election. The population parameter would be the true proportion of all eligible voters who support the candidate, while the sample statistic would be the proportion of voters who support the candidate in a particular sample of voters.
In summary, population parameters are used to describe characteristics of the entire population, while sample statistics are used to estimate these characteristics from a sample.
Sampling Methods¶
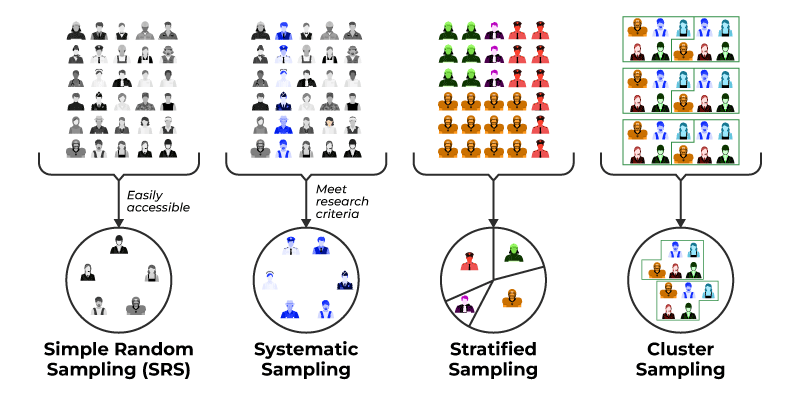
I. Probability sampling methods¶
Sampling methods refer to the techniques used to select a subset of individuals or units from a population to gather information. Here are some common sampling methods:
Simple random sampling: In this method, each individual in the population has an equal chance of being selected for the sample. This can be done using a random number generator or by using a table of random numbers.
Example: A researcher selects 100 students from a university's list of registered students by using a random number generator to pick the names.
Stratified sampling: This method involves dividing the population into subgroups or strata based on a characteristic of interest (such as age or income level) and then selecting a random sample from each stratum. This ensures that the sample is representative of the population with respect to the characteristic of interest.
Example: A pollster divides the population of a city into age groups and then selects a random sample of 50 individuals from each age group.
Cluster sampling: In this method, the population is divided into clusters or groups, and then a random sample of clusters is selected. All individuals in the selected clusters are included in the sample. This method is often used when it is difficult or costly to obtain a complete list of all individuals in the population.
Example: A public health researcher selects a random sample of 10 clinics from a list of all clinics in a particular region, and then collects data from all patients who visit those clinics during a certain period.
Systematic sampling: This method involves selecting every nth individual from a list of the population. For example, if we want to select a sample of 100 individuals from a population of 1000, we would select every 10th individual from the list.
Example: A survey researcher selects every 5th customer who enters a store during a particular hour to ask them about their shopping experience.
Convenience sampling: This method involves selecting individuals who are readily available or easy to reach, such as using participants who are nearby or who respond to an online survey. However, this method may introduce bias as the sample may not be representative of the population.
Example: A college student hands out surveys to their classmates who are available in the classroom.
Snowball sampling: This method is often used when the population is difficult to reach or identify. It involves selecting individuals who meet certain criteria and then asking them to identify others who also meet those criteria, and so on. This method can be useful for studying rare or hard-to-reach populations.
Example: A researcher studies the social networks of drug users by selecting a few initial individuals and asking them to identify other drug users they know, and so on.
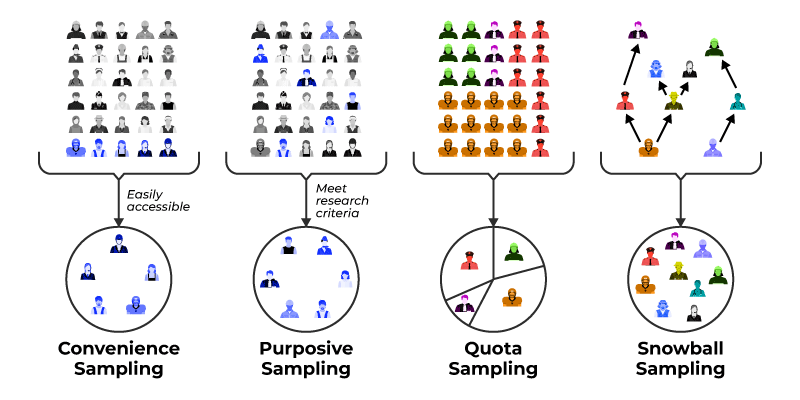
II. Non Probability sampling methods¶
Non-probability sampling methods are techniques for selecting a sample from a population in a non-random way. This means that every member of the population does not have an equal chance of being included in the sample. Non-probability sampling methods are generally used when it is difficult or impractical to obtain a random sample, such as when the population is small, hard to define, or not easily accessible. Here are some common non-probability sampling methods:
Convenience sampling: This method involves selecting individuals who are readily available or easy to reach, such as using participants who are nearby or who respond to an online survey. However, this method may introduce bias as the sample may not be representative of the population.
Example: A researcher conducts a survey on campus by handing out questionnaires to students who happen to be walking by.
Quota sampling: This method involves selecting a sample that matches certain characteristics of the population, such as age, gender, or ethnicity. The sample is selected until a predetermined number of individuals in each category are included.
Example: A market research firm wants to survey 100 individuals about a new product. They decide to include 50 men and 50 women in the sample.
Purposive sampling: This method involves selecting individuals who are believed to be typical of the population or who have specific characteristics that are of interest to the researcher.
Example: A researcher studying eating habits selects a sample of individuals who are known to be vegetarian.
Snowball sampling: This method is often used when the population is difficult to reach or identify. It involves selecting individuals who meet certain criteria and then asking them to identify others who also meet those criteria, and so on. This method can be useful for studying rare or hard-to-reach populations.
Example: A researcher studying a particular subculture selects a few initial individuals and asks them to identify other members of the subculture they know, and so on.
Judgmental sampling: This method involves selecting individuals based on the researcher's judgment and expertise about the population.
Example: A political pollster selects a sample of individuals who are likely to vote for a particular candidate based on their knowledge of the political climate.
In summary, non-probability sampling methods are useful when it is difficult or impractical to obtain a random sample. However, these methods may introduce bias and may not be representative of the population. It is important to carefully consider the strengths and limitations of different sampling methods when designing a study.
Types of data¶
Data is a specific measurement of a variable – it is the value you record in your data sheet. There are two broad categories of data: quantitative and categorical.
Quantitative data: This type of data is numerical and can be measured or counted. Quantitative data can be further divided into two subcategories: continuous and discrete.
- Continuous data: This type of data can take on any value within a range, and can be measured with a high degree of precision. Examples of continuous data include height, weight, temperature, and time.
- Discrete data: This type of data can only take on specific numerical values, and cannot be measured with the same level of precision as continuous data. Examples of discrete data include the number of children in a family, the number of cars in a parking lot, and the number of books on a shelf.
| Type of variable | What does the data represent? | Examples |
|---|---|---|
| Discrete variables (aka integer variables) | Counts of individual items or values. | Number of students in a class, Number of different tree species in a forest |
| Continuous variables (aka ratio variables) | Measurements of continuous or non-finite values. | Distance, Volume, Age |
Categorical data: This type of data is non-numerical and can be divided into categories or groups. Categorical data can be further divided into two subcategories: nominal and ordinal.
- Nominal data: This type of data consists of categories that have no inherent order or ranking. Examples of nominal data include gender, eye color, and favorite color.
- Ordinal data: This type of data consists of categories that have a specific order or ranking. Examples of ordinal data include educational level (such as high school, college, or graduate school) and Likert scales (such as strongly agree, agree, neutral, disagree, and strongly disagree).
- Binary variables: Yes or no outcomes, Examples: Heads/tails in a coin flip, Win/lose in a football game.
In summary, quantitative data consists of numerical measurements and can be continuous or discrete, while categorical data consists of non-numerical categories and can be nominal or ordinal. Understanding the type of data you have is important because it determines what statistical tests can be used and how the data should be analyzed.
Types of statistics ¶
There are two main types of statistics:
Descriptive statistics: Descriptive statistics involves the collection, organization, and presentation of data in a way that summarizes the main features of a data set. Some common descriptive statistics include
- measures of central tendency (such as the mean, median, and mode) and
- measures of variability (such as the range, variance, and standard deviation).
Inferential statistics: Inferential statistics involves making inferences or drawing conclusions about a population based on a sample of data. This involves using various statistical techniques and methods to analyze the data and draw conclusions about the population. Some common inferential statistics techniques include
- hypothesis testing,
- confidence intervals,
- regression analysis,
- ANOVA (analysis of variance), and
- correlation analysis.
In addition to these two main types of statistics, there are also other types of statistics, such as:
Biostatistics: Biostatistics is a specialized branch of statistics that deals with the analysis of data related to health and medicine.
Econometrics: Econometrics is a specialized branch of statistics that deals with the analysis of economic data.
Social statistics: Social statistics is a specialized branch of statistics that deals with the analysis of social data, such as demographics, crime rates, and education.
Business statistics: Business statistics is a specialized branch of statistics that deals with the analysis of data related to business and finance.
Overall, statistics is a broad and important field that has many different applications and types, including descriptive statistics, inferential statistics, biostatistics, econometrics, social statistics, and business statistics.
Level of Measurement¶
In statistics, the level of measurement is a classification that describes the relationship between the values of a variable.
We have four fundamental levels of measurement. They are:
Nominal level of measurement: This is the lowest level of measurement, where data is categorized into mutually exclusive categories without any order or ranking.
Examples: eye color, gender, or city or Which country do you belong to? India, Japan, Korea.
Ordinal level of measurement: Data is categorized into categories with an order or ranking. However, the distance between each category is unknown.
Examples: rankings, letter grades, or level of education or Income level – High income, medium income, low income.
Interval level of measurement: Data is measured on a scale where the distance between each point is equal, but there is no true zero point.
Examples: temperature measured in Celsius or Fahrenheit.
Ratio level of measurement: Data is measured on a scale where the distance between each point is equal, and there is a true zero point.
Examples: weight, height, or time.