Risk analysis in Banking sector¶
Author: Arun Kumar Pandey
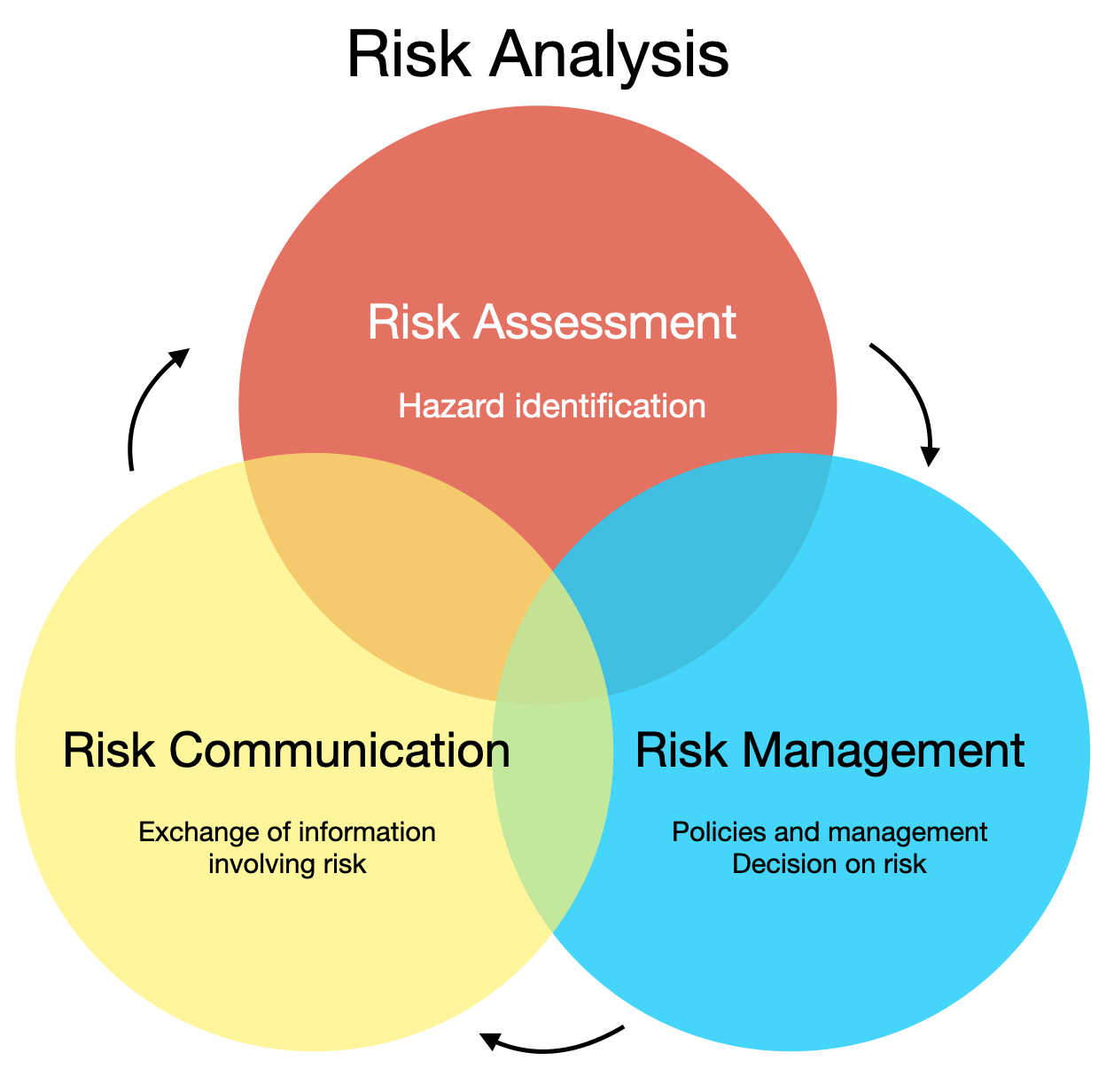
Content¶
- Risk analysis
- Various products of the banking sector
- Types of risks analyzed in finanical banking sector
- Market risk
- credit risk
- Liquidity risk
- Operational risk
- Regulatory Risk
- Reputational Risk
- Finanical Risk analysis key steps
- Market risk analysis
- Value at Risk
- Conditional Value at Risk
- Monte Carlo simulation
Risk analysis¶
Risk analysis is a process of assessing and evaluating potential risks and their impact on an organization, project, or decision-making. It involves identifying, analyzing, and prioritizing risks to make informed decisions on how to mitigate or manage them effectively.
Various products of the banking sector¶
The banking sector offers a wide range of products and services to meet the financial needs of individuals, businesses, and institutions. Here are some common products and services offered by banks:
| Sr. No. | Product name | Details |
|---|---|---|
| 1. | Deposit Accounts | savings accounts, current accounts, and fixed deposit accounts. |
| 2. | Loans and Credit Facilities | personal loans, home loans, auto loans, business loans, lines of credit, and overdraft facilities. |
| 3. | Credit Cards | Banks issue credit cards that allow individuals to make purchases on credit. |
| 4. | Debit Cards | Debit cards are linked to customers' bank accounts and allow them to make purchases and withdraw cash from ATMs. |
| 5. | Mortgages | Banks provide mortgage loans to help individuals purchase or refinance real estate properties. Mortgage loans typically have long repayment terms and are secured by the property being financed. |
| 6. | Investment Products | mutual funds, fixed-income securities, stocks, and bonds. |
| 7. | Foreign Exchange Services | Banks facilitate foreign exchange transactions, allowing customers to convert currencies for travel, international trade, or investment purposes. |
| 8. | Payment Services | online banking, mobile banking, and bill payment facilities. |
| 9. | Trade Finance | Banks offer trade finance services to facilitate international trade transactions. This includes issuing letters of credit, providing export/import financing, and managing trade-related risks. |
| 10. | Wealth Management | Banks provide wealth management services to high-net-worth individuals and institutional clients. These services include investment advisory, portfolio management, estate planning, and other customized financial solutions. |
| 11. | Insurance Products | Life insurance, health insurance, property insurance, and other types of coverage to help individuals and businesses manage risks. |
| 12. | Treasury and Cash Management Services | Banks offer treasury and cash management services to corporate clients, assisting them in managing their cash flow, optimizing liquidity, and conducting efficient financial operations. |
Types of risks analyzed in the financial banking sector¶
1. Credit risk¶
Credit risk refers to the potential for financial losses resulting from the failure of a borrower or counterparty to fulfill their financial obligations. It arises when borrowers or counterparties are unable to repay their loans or meet their contractual obligations. This risk can be mitigated through credit assessments, collateral requirements, diversification of credit exposures, and the use of credit derivatives.
Example: A bank lending money to individuals or businesses faces credit risk. If a borrower defaults on their loan payments, the bank may suffer financial losses.
Parameters used to calaculate credit risk: To calculate credit risk, several parameters are commonly used. These parameters help assess the creditworthiness of borrowers and estimate the likelihood and potential impact of default. Here are some key parameters used in credit risk analysis:
Probability of Default (PD): PD measures the likelihood that a borrower will default on their credit obligations within a specific time frame, usually expressed as a percentage. It is based on historical data, credit ratings, financial indicators, and other relevant factors.
- Historical Method: PD = (Number of Defaults within a specific time period) / (Total Number of Observations within the same time period)
- Credit Rating Transition Matrix Method: PD = (Probability of Transition from Non-Default Rating to Default Rating) * (Probability of Default Rating)
- Merton Model
Loss Given Default (LGD): LGD estimates the potential loss that a lender may incur if a borrower defaults. It represents the portion of the outstanding loan or credit exposure that is unlikely to be recovered in the event of default. LGD is typically expressed as a percentage of the exposure.
- Direct Method: LGD = (Total Exposure - Recovered Amount) / Total Exposure
- Workout Method: LGD = (Total Loss - Recovered Amount) / Total Exposure
- Statistical Method: LGD = 1 - Recovery Rate
Exposure at Default (EAD): EAD refers to the total amount of exposure that a lender has to a borrower at the time of default. It represents the maximum potential loss that can occur if a borrower defaults. EAD includes the outstanding loan balance, unused credit lines, and other forms of exposure.
- Simple Approach: EAD = Outstanding Loan Balance + Undrawn Credit Lines
- Basel Approach: EAD = Exposure Value x Credit Conversion Factor (CCF)
- Advanced Approaches
Credit Rating: Credit ratings assigned by credit rating agencies provide an indication of a borrower's creditworthiness. Ratings assess the likelihood of default and can help lenders gauge the level of credit risk associated with a borrower. Common rating scales include AAA, AA, A, BBB, BB, B, C, with each category representing different levels of creditworthiness.
Financial Ratios and Indicators: Various financial ratios and indicators are used to assess the financial health and stability of borrowers. These may include
- debt-to-equity ratio,
- current ratio,
- profitability indicators,
- cash flow analysis,
and other metrics that provide insights into the borrower's ability to meet their financial obligations.
Collateral and Guarantees: The presence of collateral or guarantees can mitigate credit risk. Collateral refers to assets provided by the borrower that can be used to recover losses in case of default. Guarantees are commitments from third parties to fulfill the borrower's obligations if they default.
Industry and Economic Factors: Credit risk analysis also considers industry-specific factors and macroeconomic conditions that may impact a borrower's ability to repay debts. Factors such as market trends, regulatory changes, and economic indicators are taken into account to evaluate credit risk.
2. Market risk¶
Market risk models and methodologies are used by financial institutions to assess and manage potential losses arising from changes in market conditions, such as fluctuations in interest rates, exchange rates, commodity prices, and equity prices. These models and methodologies help quantify and monitor market risk exposures and assist in making informed risk management decisions.
Example: An investment fund holding a portfolio of stocks is exposed to market risk. If the stock prices decline due to market downturns, the fund's value may decrease.
Here are some commonly used market risk models and methodologies:
Value at Risk (VaR): VaR is a widely used measure for estimating potential losses due to market risk. It quantifies the maximum loss within a specified confidence level (e.g., 95% or 99%) over a defined time horizon. VaR can be calculated using historical data, parametric models (such as variance-covariance models), or Monte Carlo simulations.
Expected Shortfall (ES): Also known as Conditional VaR, ES estimates the average loss beyond the VaR level. It provides additional information about the tail risk and potential losses beyond the confidence level captured by VaR.
Stress Testing: Stress testing involves subjecting a financial portfolio or institution to extreme scenarios to assess the impact on market risk exposures. Stress tests help evaluate the vulnerability of portfolios to adverse market conditions and assess capital adequacy under severe scenarios.
Historical Simulation: This method uses historical market data to estimate potential losses. It involves constructing a portfolio's profit and loss distribution based on past market movements and calculating the losses at specified confidence levels.
Monte Carlo Simulation: Monte Carlo simulation generates multiple random scenarios based on modeled assumptions for market variables. By simulating thousands of potential scenarios, it provides a distribution of possible portfolio outcomes and helps estimate potential losses.
Risk Factor Sensitivity Analysis: This analysis examines the impact of changes in individual risk factors on the portfolio's value or returns. It helps identify which market variables have the most significant influence on the portfolio's risk and allows for targeted risk management actions.
Risk Measures for Specific Instruments: Different market risk models and methodologies are used for specific financial instruments, such as interest rate risk models for fixed income securities, option pricing models for equity options, or commodity price models for commodity derivatives. These models consider the unique characteristics and sensitivities of each instrument to assess market risk exposures.
Value Adjustments (XVA): XVAs are adjustments made to the value of derivatives and other financial instruments to account for counterparty credit risk, funding costs, and other risk factors. XVAs are calculated using models that incorporate market risk factors along with credit risk and funding cost components.
3. Liquidity risk¶
Liquidity risk refers to the potential difficulty of buying or selling an investment quickly and at a fair price without causing significant price changes. It arises from insufficient market liquidity or an inability to convert assets into cash when needed. Liquidity risk can be managed by maintaining adequate cash reserves, diversifying funding sources, and establishing contingency funding plans.
Example: A mutual fund holding illiquid assets, such as real estate or private equity, may face liquidity risk if investors want to redeem their shares, but the fund struggles to sell the underlying assets quickly.
4. Operational risk¶
Operational risk is the potential for losses resulting from inadequate or failed internal processes, systems, human errors, or external events. It encompasses risks related to technology, fraud, legal compliance, and business continuity. Operational risk can be mitigated through proper internal controls, staff training, disaster recovery plans, and risk monitoring.
Example: A cyber-attack on a financial institution's systems that compromises customer data and disrupts operations represents operational risk.
5. Regulatory Risk¶
Regulatory risk arises from changes in laws, regulations, or government policies that impact the financial industry. It includes the risk of non-compliance with applicable regulations, which can lead to financial penalties, reputational damage, or restrictions on business activities. Regulatory risk can be managed through robust compliance programs, staying updated on regulatory changes, and engaging with regulatory authorities.
Example: A bank faces regulatory risk if new legislation imposes stricter capital requirements, necessitating adjustments to its operations and capital structure.
6. Reputational Risk¶
Reputational risk refers to the potential loss of reputation or public trust in an organization due to negative perceptions or events. It arises from actions, behaviors, or incidents that damage the public image or brand value. Reputational risk can be mitigated by maintaining high ethical standards, providing quality products/services, effective crisis management, and transparent communication with stakeholders.
Example: A scandal involving unethical practices in a financial institution can result in reputational risk, leading to customer loss, decreased investor confidence, and legal consequences.
Financial Risk Analysis key steps¶
The process of risk analysis in the financial banking sector involves several key steps. While the specific approach may vary among institutions, here are the common steps typically followed in conducting risk analysis:
1. Risk Identification:¶
The first step is to identify and document the various risks that the bank is exposed to. This includes examining potential risks related to credit, market, liquidity, operational, compliance, and reputational factors. Risk identification involves reviewing
Internal Data Analysis: Analyzing historical data within the institution can help identify patterns, trends, and potential risks. This includes reviewing past incidents, losses, and near-miss events to identify areas where risks have materialized or have the potential to occur in the future.
External Research and Industry Analysis: Conducting research and staying updated on industry trends, market conditions, regulatory changes, and emerging risks can provide valuable insights into potential risks that may impact the financial sector. External sources such as industry reports, market studies, regulatory announcements, and news sources can be used for this purpose.
Risk Registers and Checklists: Using predefined risk registers and checklists can help systematically identify risks across different areas of banking operations. These tools typically cover a wide range of risk categories, including credit risk, market risk, operational risk, compliance risk, and liquidity risk, prompting risk managers to consider specific risk factors relevant to their institution.
Risk Workshops and Brainstorming: Conducting risk workshops and brainstorming sessions involving key stakeholders can provide a platform for collaborative discussions on potential risks. These sessions allow participants to share their expertise, experiences, and insights to identify risks that may not be apparent through other methods. Facilitated discussions can encourage a comprehensive examination of risks from different perspectives.
Scenario Analysis and Stress Testing: By simulating various scenarios and stress tests, institutions can identify risks that may arise under adverse conditions. This involves modeling different economic, financial, and operational scenarios to evaluate their impact on the institution's financial position, profitability, and risk exposure. Stress testing helps identify vulnerabilities and assess the resilience of the institution to withstand adverse events.
Regulatory and Compliance Analysis: Staying updated on regulatory requirements and compliance obligations is essential for identifying risks related to legal and regulatory compliance. Analyzing regulatory changes, enforcement actions, and compliance failures in the industry can provide insights into potential risks and areas where the institution may be exposed to compliance-related issues.
Risk Indicators and Key Risk Indicators (KRIs): Developing and monitoring risk indicators and KRIs can help identify early warning signals of potential risks. These indicators are specific metrics or measures that are closely linked to the occurrence or amplification of risks. By establishing thresholds and monitoring deviations, institutions can identify and address risks before they escalate.
Risk Assessments and Audits: Conducting regular risk assessments and internal audits can help identify risks by systematically reviewing and evaluating different areas of the institution's operations. Risk assessments involve reviewing processes, controls, and risk management frameworks to identify gaps or weaknesses that could expose the institution to risks.
2. Risk Assessment:¶
Once the risks are identified, the next step is to assess their potential impact and likelihood of occurrence. This involves quantifying and qualifying the risks based on historical data, statistical analysis, industry benchmarks, and expert judgment. The goal is to understand the severity of each risk and prioritize them based on their significance to the bank's operations and objectives.
Risk analysis is used in risk analysis to quantify and analyze various types of risks in finance. Here's how it is applied in risk analysis:
| Application | Used for | Factors used or used for |
|---|---|---|
| Assessing portfolio risk | to know risk and volatility of investment protfolios | VaR, ES, CVaR |
| Scenario Analysis | to know the future sceanrios and hence impact on future outcomes | market conditions, interest rates, exchange rates, or macroeconomic variables |
| Stress Testing | to evaluate the resilience of financial institutions or portfolios under adverse conditions | vulnerabilities, evaluate worst-case scenarios, and design risk mitigation strategies |
| Risk Mitigation Strategies | helps in evaluating and comparing different risk mitigation strategies | diversification, hedging, or asset allocation adjustments |
| Credit Risk Analysis | to estimate credit-related metrics such as Probability of Default (PD), Loss Given Default (LGD), or Credit Value-at-Risk (CVaR) | it helps assess the credit risk of individual loans or credit portfolios by considering default correlations, recovery rates, or credit rating migrations |
Above table can be explained in more details as:
Assessing Portfolio Risk: Monte Carlo simulation is used to estimate the potential risk and volatility of investment portfolios. By simulating thousands or millions of potential market scenarios, it generates a distribution of portfolio returns. This allows risk analysts to calculate risk metrics such as Value-at-Risk (VaR), Expected Shortfall (ES), or Conditional Value-at-Risk (CVaR) at different confidence levels. These metrics provide insights into the potential downside risk and help investors make informed decisions regarding portfolio diversification, risk tolerance, and hedging strategies.
Scenario Analysis: Monte Carlo simulation enables risk analysts to perform scenario analysis by simulating a range of possible future scenarios and evaluating their impact on financial outcomes. This involves considering multiple factors such as market conditions, interest rates, exchange rates, or macroeconomic variables. By incorporating these variables into the simulation, analysts can assess the potential effects of different scenarios on key performance indicators, cash flows, or profitability measures.
Stress Testing: Monte Carlo simulation is used in stress testing exercises to evaluate the resilience of financial institutions or portfolios under adverse conditions. It involves simulating extreme scenarios, such as market crashes, economic recessions, or liquidity shocks, to assess the impact on risk exposures, capital adequacy, or liquidity positions. By stress testing using Monte Carlo simulation, risk analysts can identify vulnerabilities, evaluate worst-case scenarios, and design risk mitigation strategies.
Risk Mitigation Strategies: Monte Carlo simulation helps in evaluating and comparing different risk mitigation strategies. By simulating the effectiveness of various risk management techniques, such as diversification, hedging, or asset allocation adjustments, it enables risk analysts to quantify the potential impact of these strategies on risk reduction. This allows decision-makers to make informed choices and implement risk mitigation measures based on the simulation results.
Credit Risk Analysis: Monte Carlo simulation is employed in credit risk analysis to estimate credit-related metrics such as Probability of Default (PD), Loss Given Default (LGD), or Credit Value-at-Risk (CVaR). By simulating potential default scenarios and incorporating factors such as default correlations, recovery rates, or credit rating migrations, it helps assess the credit risk of individual loans or credit portfolios. This information is crucial for credit risk management, loan pricing, and the calculation of regulatory capital requirements.
3. Risk Measurement and Quantification:¶
This step involves measuring and quantifying the identified risks in monetary terms or other relevant units of measurement. Here are some common measures for risk in the financial sector:
Value-at-Risk (VaR): VaR is a widely used measure that estimates the potential loss in the value of a portfolio or position over a specified time horizon at a certain level of confidence. It provides an estimate of the maximum loss that an organization may face under normal market conditions. VaR is commonly used to measure market risk.
Expected Loss (EL): Expected Loss is a measure that estimates the average loss that an organization is likely to experience from a particular risk. It considers both the probability of occurrence and the potential impact of the risk. Expected Loss is often used to assess credit risk.
Conditional Value-at-Risk (CVaR): CVaR, also known as Expected Shortfall (ES), is a measure that provides an estimate of the expected loss beyond the VaR level. It quantifies the potential losses in the tail of the risk distribution, capturing the severity of extreme events. CVaR is useful for assessing risks associated with rare or extreme events.
Risk-adjusted Return on Capital (RAROC): RAROC is a measure that evaluates the risk-adjusted profitability of an investment or business line. It considers the potential returns generated by the investment relative to the risks taken. RAROC helps in assessing the efficiency of capital allocation and supporting decision-making on resource allocation.
Key Risk Indicators (KRIs): KRIs are specific metrics or indicators used to monitor and measure risks. They act as early warning signals by highlighting deviations from normal risk levels or thresholds. KRIs are tailored to specific risk types and provide ongoing monitoring of risks.
Credit Ratings: Credit ratings assigned by credit rating agencies are measures of credit risk associated with financial instruments, such as corporate bonds, sovereign debt, or structured products. These ratings assess the creditworthiness and likelihood of default of the issuer, providing an indication of the credit risk involved.
Loss Given Default (LGD): LGD is a measure that quantifies the potential loss a lender may face if a borrower defaults on a loan or credit obligation. It represents the portion of the exposure that is unlikely to be recovered in the event of default.
Capital Adequacy Ratios: Capital adequacy ratios, such as the Basel III regulatory framework's Common Equity Tier 1 (CET1) ratio, measure the financial institution's capital reserves relative to its risk-weighted assets. These ratios help assess the organization's ability to absorb losses and meet regulatory capital requirements.
Operational Risk Indicators: Operational risk indicators measure risks associated with internal processes, systems, and people. They capture metrics such as the frequency of operational incidents, the time taken to resolve issues, or the level of compliance with internal controls. Operational risk indicators help monitor and manage operational risks.
Stress Testing Results: Stress testing involves subjecting financial institutions' portfolios and balance sheets to extreme scenarios or stress events. The results of stress tests provide insights into the potential impact of adverse events on the organization's financial health and resilience.
4. Risk Monitoring and Reporting:¶
Once risks are identified and measured, it is crucial to establish monitoring mechanisms to track their evolution over time. Regular monitoring allows banks to detect changes in risk levels, identify emerging risks, and take timely actions. Risk reporting is an essential component, providing key stakeholders with transparent and accurate information on the bank's risk profile, exposures, and mitigation strategies.
Risk Monitoring: Risk monitoring involves ongoing surveillance and analysis of market risks. It includes:
- Regular Portfolio Reviews: Periodic assessment of investment portfolios to ensure they align with the risk tolerance and investment objectives of investors.
- Monitoring Market Indicators: Tracking relevant market indicators such as stock indices, interest rates, or exchange rates to identify potential risks or market trends.
- Real-time Reporting: Utilizing technology and risk management systems to provide real-time updates on market positions and risk exposures.
5. Risk Mitigation and Management:¶
After assessing risks and monitoring their status, banks need to develop strategies to mitigate and manage the identified risks effectively. This may involve implementing risk controls, establishing risk limits, diversifying portfolios, enhancing internal processes, implementing risk transfer mechanisms (such as insurance), and creating contingency plans. Risk mitigation strategies should align with the bank's risk appetite and regulatory requirements.
Risk Mitigation: Risk mitigation strategies aim to reduce the impact of market risks on investments. Here are some common risk mitigation techniques:
- Diversification: Spreading investments across different asset classes, sectors, or geographic regions can help reduce concentration risk. If one investment performs poorly, others may provide a buffer.
- Hedging: Using derivative instruments like options, futures, or swaps can hedge against adverse price movements. For example, buying a put option can protect against a decline in the value of a stock.
- Dynamic Asset Allocation: Regularly adjusting portfolio allocations based on market conditions can help reduce risk exposure. For instance, shifting investments from equities to bonds during periods of high market volatility.
6. Risk Communication and Governance:¶
Effective risk analysis involves robust communication and governance structures. Banks should establish clear lines of responsibility and accountability for managing risks. Regular communication among risk management teams, senior management, and the board of directors is necessary to ensure a comprehensive understanding of risks and to facilitate informed decision-making.
- Capital Adequacy: Compliance with regulatory capital requirements to ensure sufficient capital buffers are maintained to absorb potential losses.
- Reporting and Disclosure: Providing accurate and timely reporting on risk exposures, market positions, and risk management strategies to regulatory authorities.
- Risk Governance: Establishing robust risk governance frameworks, policies, and procedures to ensure effective risk management and compliance.
7. Regular Review and Update¶
Risk analysis is an ongoing process that requires regular review and update. Banks should periodically reassess risks to reflect changes in the business environment, market conditions, regulatory requirements, and internal operations. This iterative process helps ensure that risk analysis remains relevant and effective in addressing the evolving risk landscape.
8. Risk reduction strategies¶
To reduce risk in investments, a combination of strategies can be employed:
- Diversify: Invest in a mix of asset classes (stocks, bonds, real estate) to spread risk.
- Set Risk Tolerance: Determine your risk tolerance and invest accordingly. This ensures that investments align with your risk appetite.
- Regular Monitoring: Keep track of market trends and portfolio performance to make informed decisions.
- Stay Informed: Stay updated on economic indicators, market news, and industry developments that can impact investments.
- Consult with Professionals: Seek advice from financial advisors or professionals who specialize in risk management and investment strategies.
It is important to note that the risk cannot be eliminated entirely, but by employing prudent risk management techniques, investors can aim to minimize potential losses and optimize their investment outcomes.
1. Value-at-Risk (VaR)
"Value-at-Risk (VaR) is a widely used measure in risk management that estimates the potential loss in the value of a portfolio or position over a specified time horizon at a certain level of confidence."
OR
"The maximum loss in a given holding period to a certain confidence level."
It provides an estimate of the maximum loss that an organization may face under normal market conditions.
There are several methods to calculate VaR
- Historical VaR:
Historical VaR is based on historical data and does not rely on any specific distribution assumption. The historical method looks at one’s prior returns history and orders them from worst losses to greatest gains—following from the premise that past returns experience will inform future outcomes. It calculates VaR using the historical distribution of portfolio returns. The formula for Historical VaR is:
Historical VaR = Portfolio Value * (1 - Confidence Level) * Return at the Selected Percentile
where:
- VaR: Value-at-Risk
- Portfolio Value: Total value of the portfolio being assessed
- Historical Return Percentile::The desired percentile of the historical return distribution, typically based on a confidence level (e.g., 95%, 99%).
- VaR: Value-at-Risk
where:
- VaR: Value-at-Risk
- Portfolio Value: Total value of the portfolio being assessed
- z-score: The number of standard deviations corresponding to the desired level of confidence. For example, for a 95% confidence level, the z-score is 1.96.
- Standard Deviation: The standard deviation of the portfolio returns, which represents the portfolio's volatility.
where:
- VaR: Value-at-Risk
- Portfolio Value: Total value of the portfolio being assessed
- Confidence Level: The desired level of confidence (e.g., 95%, 99%)
- Simulated Returns:A large number of simulated returns generated based on assumed or estimated distributions of asset returns.
- Historical Return Percentile::The desired percentile of the historical return distribution, typically based on a confidence level (e.g., 95%, 99%).
Importance:The value of VaR represents the potential loss or downside risk associated with a portfolio or position.
- A higher VaR value indicates a greater potential loss, indicating a higher level of risk.
- Conversely, a lower VaR value suggests a lower potential loss and, therefore, a lower level of risk.
===> What number are you able to cope with to a given amount of certainity over given amount of time period/holding period as a loss level. So let's say that at 90% percentile. SO 95% chance that my profit is going to be above this value that we are calculating i.e. this Var.
===> So we want to be able to say that $95\%$ certainty that our 'Value at Risk (Var)' will not exceed a certain value.
====> What number are you able to cope with to a given amount of certainity or a given amount of time
===> So Var is associated with maximum loss over a given period of time to a given confidence level.
Example¶
Calculation of parametric VaR and historical VaR
Let's assume you have daily returns for investment over the past 1,000 trading days. You want to calculate the 95% VaR for a $100,000 investment.
- Step 1: Gather the historical returns data.
- Step 2: Order the historical returns in descending order.
- Step 3: Choose the VaR level (e.g., 95%).
- Step 4: Identify the VaR value by locating the return corresponding to the 95th percentile in the ordered return series.
import numpy as np
import pandas as pd
# Assuming you have the daily returns data as an array called 'returns'
returns = [0.01, -0.02, 0.03, -0.01] # Replace with your actual data
# Specify the confidence level (95%)
confidence_level = 0.95
# Calculate the portfolio value
portfolio_value = 100000
# Sort the returns in ascending order
sorted_returns = sorted(returns)
# Determine the index corresponding to the desired percentile
index = int((1 - confidence_level) * len(sorted_returns))
# Retrieve the historical return at the determined index
historical_return = sorted_returns[index]
# Calculate VaR using Historical VaR formula
historical_var = -portfolio_value * historical_return
# Calculate the weighted returns of each asset
weights = np.array([1 / len(returns)] * len(returns))
weighted_returns = np.multiply(returns, weights)
# Calculate the portfolio return
portfolio_return = np.sum(weighted_returns)
# Print the results
print("Historical VaR at", confidence_level * 100, "% confidence level:", historical_var)
print("Portfolio Return:", portfolio_return)
Historical VaR at 95.0 % confidence level: 2000.0 Portfolio Return: 0.002499999999999999
means total loss....
# Parameter VaR: example
import numpy as np
from scipy.stats import norm
def calculate_var(portfolio_value, returns, confidence_level):
# Calculate portfolio returns' standard deviation
returns_std = np.std(returns)
# Determine the z-score corresponding to the desired confidence level
z_score = norm.ppf(1 - confidence_level)
# Calculate VaR using the Parametric VaR formula
var = portfolio_value * z_score * returns_std
return var
# Example usage
portfolio_value = 100000 # Total portfolio value
returns = np.array([0.01, -0.02, 0.03, -0.01]) # Sample returns data
confidence_level = 0.95 # Confidence level of 95%
par_var = - calculate_var(portfolio_value, returns, confidence_level)
print("VaR at 95% confidence level:", par_var)
VaR at 95% confidence level: 3158.5901106311394
Monte Carlo Simulation to calculate VaR and CVaR¶
Monte Carlo Simulation is a versatile and powerful tool in the financial sector. Here are some of the applications and use cases where Monte Carlo Simulation can be utilized:
Portfolio Optimization: Monte Carlo Simulation can be used to optimize investment portfolios by simulating various asset allocation strategies. By generating random samples of asset returns, the simulation can estimate the expected portfolio returns, risk measures such as standard deviation or Value at Risk (VaR), and optimize the portfolio composition to maximize return or minimize risk.
Option Pricing: Monte Carlo Simulation is widely employed in option pricing models, such as the Black-Scholes model. By simulating the future stock price movements based on random samples, the simulation can estimate the option's value and evaluate different option trading strategies.
Risk Management: Monte Carlo Simulation is valuable in assessing and managing risks in the financial sector. It can be used to simulate market risks, credit risks, operational risks, and other types of risks. By generating random scenarios, the simulation can quantify the potential losses, estimate risk measures such as Value at Risk (VaR) or Expected Shortfall (ES), and evaluate risk mitigation strategies.
Financial Planning: Monte Carlo Simulation can aid in financial planning and retirement analysis. By incorporating variables like income, expenses, investment returns, and lifespan, the simulation can generate random scenarios of future financial situations. This helps individuals or financial advisors make informed decisions about saving, spending, and investment strategies.
Stress Testing: Monte Carlo Simulation is utilized for stress testing financial systems and institutions. By simulating extreme scenarios and generating random samples of variables like market shocks or defaults, the simulation can evaluate the resilience and stability of financial systems, identify potential vulnerabilities, and inform regulatory decision-making.
Credit Risk Assessment: Monte Carlo Simulation can be applied to credit risk assessment, especially for loan portfolios and credit derivatives. By simulating default events and loss given default, the simulation can estimate credit risk measures, such as expected loss or probability of default, and evaluate credit portfolio performance under different scenarios.
These are just a few examples of how Monte Carlo Simulation can be employed in the financial sector. Its flexibility and ability to capture uncertainty make it a valuable tool for risk assessment, decision-making, and strategic planning in finance.
Example on Monte Carlo Simulation¶
1. normal distribution¶
# Monte carlo simulation using normal distribution
import numpy as np
import pandas as pd
# Example portfolio simulation using Monte Carlo
num_simulations = 10000
portfolio_value = 1000000
initial_investment = 1000000
expected_return = 0.08 # 8% return
volatility = 0.2
# Generate random returns based on normal distribution
returns = np.random.normal(expected_return, volatility, num_simulations)
# Calculate portfolio values for each simulation
portfolio_values = initial_investment * (1 + returns)
# Sort the simulated portfolio values
sorted_portfolio_values = np.sort(portfolio_values)
# Define the desired confidence level (e.g., 95%)
confidence_level = 0.95
# Calculate the VaR at the desired confidence level
percentile = 1 - confidence_level
index = int(percentile * num_simulations)
var = initial_investment - sorted_portfolio_values[index]
# Create a dataframe to store the portfolio returns
df_portfolio_returns = pd.DataFrame({'Portfolio Return': portfolio_values})
# Print the result
print("VaR at", confidence_level * 100, "% confidence level:", var)
print("Portfolio return for each simulation:\n", df_portfolio_returns)
VaR at 95.0 % confidence level: 242443.6554306997
Portfolio return for each simulation:
Portfolio Return
0 9.818251e+05
1 1.174371e+06
2 1.006901e+06
3 1.037849e+06
4 1.167950e+06
... ...
9995 1.129363e+06
9996 1.470854e+06
9997 1.229015e+06
9998 1.514311e+06
9999 1.223820e+06
[10000 rows x 1 columns]
import matplotlib.pyplot as plt
# Plot histogram of portfolio returns
plt.figure(figsize=(10, 6))
plt.hist(portfolio_values, bins=50, color='skyblue', edgecolor='black')
plt.axvline(var, color='red', linestyle='dashed', linewidth=2, label='VaR at 95%')
plt.xlabel('Portfolio Return')
plt.ylabel('Frequency')
plt.title('normal-Distribution of Portfolio Returns')
plt.legend()
plt.grid(True)
plt.show()
2. t-distribution for returns¶
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Example portfolio simulation using Monte Carlo
num_simulations = 10000
portfolio_value = 1000000
initial_investment = 1000000
expected_return = 0.08 # 8% return
volatility = 0.2
# Generate random returns based on t-distribution
degrees_of_freedom = 10 # Adjust the degrees of freedom as needed
returns1 = np.random.standard_t(degrees_of_freedom, num_simulations)
# Calculate portfolio values for each simulation
portfolio_values1 = initial_investment * (1 + returns1)
# Sort the simulated portfolio values
sorted_portfolio_values1 = np.sort(portfolio_values1)
# Define the desired confidence level (e.g., 95%)
confidence_level = 0.95
# Calculate the VaR at the desired confidence level
percentile = 1 - confidence_level
index = int(percentile * num_simulations)
tvar = initial_investment - sorted_portfolio_values1[index]
# Create a dataframe to store the portfolio returns
df_portfolio_returns1 = pd.DataFrame({'Portfolio Return': portfolio_values1})
# Print the result
print("VaR at", confidence_level * 100, "% confidence level:", tvar)
print("Portfolio return for each simulation:\n", df_portfolio_returns1)
# Plot histogram of portfolio returns
plt.figure(figsize=(10, 6))
plt.hist(portfolio_values1, bins=50, color='skyblue', edgecolor='black')
plt.axvline(tvar, color='red', linestyle='dashed', linewidth=2, label='t-distribution VaR at 95%')
plt.axvline(var, color='blue', linestyle=':', linewidth=2, label='normal-distribution VaR at 95%') # calculated previosuly
plt.xlabel('Portfolio Return')
plt.ylabel('Frequency')
plt.title('t-Distribution of Portfolio Returns')
plt.legend()
plt.grid(True)
plt.show()
VaR at 95.0 % confidence level: 1808807.650447472
Portfolio return for each simulation:
Portfolio Return
0 1.610446e+06
1 2.395520e+06
2 3.708464e+04
3 5.411488e+05
4 1.569818e+06
... ...
9995 1.827206e+06
9996 -4.927888e+05
9997 9.117096e+05
9998 -8.892813e+04
9999 -2.222589e+05
[10000 rows x 1 columns]
Consulsion:¶
If the calculated VaR is lower than the historical returns, it suggests that the estimated potential loss (VaR) at the specified confidence level is less than the actual historical returns observed in the portfolio.
This situation indicates that, based on the given confidence level, the portfolio has historically experienced returns that are higher than the estimated potential loss. In other words, the portfolio has historically performed better than what the VaR calculation predicts in terms of downside risk.
From a risk management perspective, this could be seen as a positive outcome as it suggests that the portfolio has been able to generate higher returns compared to the estimated downside risk. However, it's important to note that past performance does not guarantee future results, and the historical returns alone may not be a reliable indicator of future performance.
It's crucial to consider other risk measures and conduct a comprehensive risk analysis to assess the overall risk profile of the portfolio. Additionally, the VaR calculation should be reviewed and validated to ensure it accurately reflects the portfolio's risk exposure and incorporates relevant factors.
2. Expected Loss (EL)
Expected Loss (EL) is a risk measure used in financial analysis to estimate the average or expected amount of loss that an organization or portfolio is likely to experience over a given time period. It combines the probability of various loss scenarios with the corresponding potential losses.
- The formula to calculate Expected Loss (EL) is:
- Probability of Default (PD) represents the likelihood or probability that a borrower or counterparty will default on their obligations within a specified time horizon.
- Exposure at Default (EAD) refers to the amount of exposure or the total value of outstanding loans or commitments at the time of default.
- Loss Given Default (LGD) represents the percentage or proportion of the exposure that is expected to be lost in the event of default.
- By multiplying these three factors, the formula estimates the average loss expected for a specific counterparty or portfolio.
- It's important to note that Expected Loss is just one component of the broader credit risk assessment process. It provides a useful measure to assess the potential credit losses and make informed decisions regarding credit risk management, loan provisioning, capital allocation, and pricing of credit products.
where:
3. Conditional Value-at-Risk (CVaR)
Conditional Value-at-Risk (CVaR), also known as Expected Shortfall (ES), is a risk measure that quantifies the expected loss beyond a certain confidence level. Unlike Value-at-Risk (VaR), which only provides information about the worst-case loss at a specific confidence level, CVaR provides an estimate of the average loss that may occur in the tail of the distribution beyond the VaR threshold.
- The formula to calculate CVaR is as follows::
- Probability of Default (PD) represents the likelihood or probability that a borrower or counterparty will default on their obligations within a specified time horizon.
- Exposure at Default (EAD) refers to the amount of exposure or the total value of outstanding loans or commitments at the time of default.
- Loss Given Default (LGD) represents the percentage or proportion of the exposure that is expected to be lost in the event of default.
- By multiplying these three factors, the formula estimates the average loss expected for a specific counterparty or portfolio.
- It's important to note that Expected Loss is just one component of the broader credit risk assessment process. It provides a useful measure to assess the potential credit losses and make informed decisions regarding credit risk management, loan provisioning, capital allocation, and pricing of credit products.
$\text{CVaR} = \frac{1}{1 - \alpha} \int_{\alpha}^{1} f(x) \cdot x \, dx$
4.1. Example (Growth or decline of an investment)¶
To calculate the growth or decline of an investment over time, you can use the compound interest formula. The formula for calculating the future value of an investment with compound interest is:
$\text{FV} = \text{PV}\times \left(1+r\right)^n$.
Where:
- $\text{FV}$ is the future value of the investment,
- $\text{PV}$ is the present value or initial investment amount,
- $r$ is the annual interest rate (expressed as a decimal),
- $n$ is the number of compounding periods (in this case, the number of years).
Using this formula, you can calculate the growth or decline of an investment over time. Here's how it applies to the Monte Carlo Simulation example:
In each simulation of the Monte Carlo Simulation, we calculate the investment value for each year based on the generated random returns.
Let's consider a specific year in the investment period, denoted by
year.initial_investment: The initial investment amount (PV).annual_return: The generated random return for that year (r).investment_value: The investment value for that year in the simulation (FV).
The formula for calculating the investment value based on compound interest is:
$\boxed{\text{investment\_value} = \text{initial\_investment}×(1+\text{annual\_return})^{\text{year}}}$
This formula calculates the investment value at a specific year based on the initial investment amount and the generated random return for that year. The calculation is done for each year in the investment period and for each simulation.
Generating random samples for the annual returns is a key step in Monte Carlo Simulation. Here's why we generate random samples:
Uncertainty Modeling: In many real-world scenarios, future outcomes or returns are uncertain and can vary. By generating random samples for the annual returns, we are introducing variability and capturing the uncertainty associated with the investment's performance. Each random sample represents a potential outcome or scenario.
Probability Distribution: The random samples are generated based on a specified probability distribution, often the normal distribution. The choice of the distribution depends on the characteristics of the data and the assumptions made. By generating random samples from the distribution, we can simulate a range of potential returns, accounting for both positive and negative outcomes.
Multiple Simulations: Monte Carlo Simulation typically involves running multiple simulations to obtain a more comprehensive understanding of the possible outcomes. Each simulation consists of a set of random samples representing the annual returns. By running numerous simulations with different random samples, we can explore a wide range of potential scenarios and obtain a statistical distribution of the investment's performance.
Statistical Analysis: After performing the simulations, we can analyze the results to derive meaningful insights and assess the risk associated with the investment. The statistical analysis involves calculating various measures such as mean, standard deviation, percentiles, and confidence intervals. These statistics provide information about the expected value, variability, and potential downside risks of the investment.
Overall, generating random samples for the annual returns allows us to model uncertainty, simulate different scenarios, and analyze the range of possible outcomes. It enables us to make more informed decisions, evaluate risks, and understand the distribution of potential investment performance. The formula used to generate the random samples:
$(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}$
Where:
xis the random variable (in this case, the annual return).\muis the mean or expected value of the distribution (in this case,annual_return).\sigmais the standard deviation of the distribution (in this case,volatility).
The formula generates random samples by randomly selecting values from the normal distribution with the specified mean (annual_return) and standard deviation (volatility).
To generate the random samples, the formula uses the np.random.normal function from the NumPy library, which internally applies this mathematical formula to generate random numbers following a normal distribution.
Note that the formula calculates the probability density for a specific value x in the distribution, but in the context of the Monte Carlo Simulation, we are generating random samples of annual returns (x) rather than calculating the probability density.
import numpy as np
# Define variables and assumptions
initial_investment = 10000
annual_return = 0.08
volatility = 0.15
investment_period = 10
num_simulations = 1000
# Generate random samples
random_returns = np.random.normal(annual_return, volatility, size=(num_simulations, investment_period))
# Perform simulations
investment_values = initial_investment * np.cumprod(1 + random_returns, axis=1)
# Analyze the results
mean_value = np.mean(investment_values, axis=0)
std_dev = np.std(investment_values, axis=0)
lower_bound = np.percentile(investment_values, 5, axis=0)
upper_bound = np.percentile(investment_values, 95, axis=0)
# Print the results
for year in range(investment_period):
print(f"Year {year+1}: Mean Value = {mean_value[year]:.2f}, "
f"Standard Deviation = {std_dev[year]:.2f}, "
f"5th Percentile = {lower_bound[year]:.2f}, "
f"95th Percentile = {upper_bound[year]:.2f}")
Year 1: Mean Value = 10753.88, Standard Deviation = 1507.84, 5th Percentile = 8378.93, 95th Percentile = 13330.71 Year 2: Mean Value = 11626.91, Standard Deviation = 2249.23, 5th Percentile = 8149.32, 95th Percentile = 15489.35 Year 3: Mean Value = 12484.33, Standard Deviation = 3032.10, 5th Percentile = 8062.11, 95th Percentile = 17936.62 Year 4: Mean Value = 13488.37, Standard Deviation = 3770.08, 5th Percentile = 8140.69, 95th Percentile = 20431.44 Year 5: Mean Value = 14596.07, Standard Deviation = 4675.40, 5th Percentile = 8409.10, 95th Percentile = 23031.90 Year 6: Mean Value = 15643.68, Standard Deviation = 5445.60, 5th Percentile = 8090.07, 95th Percentile = 25758.89 Year 7: Mean Value = 16890.48, Standard Deviation = 6317.47, 5th Percentile = 8202.91, 95th Percentile = 28733.80 Year 8: Mean Value = 18143.62, Standard Deviation = 7261.77, 5th Percentile = 8454.08, 95th Percentile = 32171.58 Year 9: Mean Value = 19423.36, Standard Deviation = 8092.34, 5th Percentile = 8939.32, 95th Percentile = 34924.04 Year 10: Mean Value = 21043.29, Standard Deviation = 9202.29, 5th Percentile = 9193.58, 95th Percentile = 38983.00
Define variables and assumptions:
- initial_investment: The initial investment amount (e.g., $10,000).
- annual_return: The expected annual return on the investment (e.g., 0.08 or 8%).
- volatility: The standard deviation of the annual returns, representing the investment's volatility (e.g., 0.15 or 15%).
- investment_period: The number of years for which we want to simulate the investment (e.g., 10).
- num_simulations: The number of simulations to run (e.g., 1000).
Generate random samples:
We use the normal distribution to generate random samples of annual returns for each year of the investment period. The mean of the distribution is the annual_return, and the standard deviation is the volatility. We generate num_simulations random samples for each year.
Perform simulations:
We perform simulations by calculating the investment value for each year based on the generated random returns. We use the np.cumprod() function from the NumPy library to calculate the cumulative product of (1 + random_returns) for each year, representing the growth or decline of the investment over time. We multiply this with the initial_investment to get the investment value for each simulation and each year.
Analyze the results:
We analyze the results by calculating statistics for each year of the investment period. We calculate the mean value, standard deviation, and percentiles (5th and 95th) of the investment values across all simulations for each year.
Print the results:
Finally, we print the calculated statistics for each year of the investment period, including the mean value, standard deviation, and percentiles (5th and 95th). This gives us an understanding of the range of possible outcomes and the level of uncertainty associated with the investment value over time.
Portfolio optimization¶
import numpy as np
# Define the portfolio assets and their expected returns and covariance matrix
assets = ['Asset1', 'Asset2', 'Asset3']
expected_returns = np.array([0.1, 0.15, 0.12])
cov_matrix = np.array([[0.05, 0.02, 0.01],
[0.02, 0.08, 0.03],
[0.01, 0.03, 0.06]])
# Define the number of simulations and portfolio size
num_simulations = 10000
portfolio_size = len(assets)
# Generate random portfolio weights
weights = []
for _ in range(num_simulations):
w = np.random.random(portfolio_size)
w /= np.sum(w)
weights.append(w)
weights = np.array(weights)
# Calculate portfolio returns and volatility for each simulation
portfolio_returns = np.dot(weights, expected_returns)
portfolio_volatility = np.sqrt(np.dot(weights, np.dot(cov_matrix, weights.T)))
# Find the optimal portfolio with maximum Sharpe Ratio
optimal_portfolio_index = np.where(portfolio_returns / portfolio_volatility == np.max(portfolio_returns / portfolio_volatility))[0][0]
# Get the optimal portfolio weights and performance measures
optimal_weights = weights[optimal_portfolio_index]
optimal_returns = portfolio_returns[optimal_portfolio_index]
optimal_volatility = portfolio_volatility[optimal_portfolio_index]
# Print the optimal portfolio weights and performance measures
print("Optimal Portfolio Weights:")
for asset, weight in zip(assets, optimal_weights):
print(f"{asset}: {weight:.2f}")
print("\nOptimal Portfolio Performance:")
print("Expected Return:", optimal_returns)
print("Volatility:", optimal_volatility)
Optimal Portfolio Weights: Asset1: 0.96 Asset2: 0.03 Asset3: 0.01 Optimal Portfolio Performance: Expected Return: 0.10172249180875181 Volatility: [0.17002804 0.16831453 0.16861898 ... 0.1902971 0.16490089 0.15897608]
REFERENCE¶
- https://medium.com/@arunp77/data-science-and-risk-analysis-in-the-financial-banking-38bb27f64a9c
- https://analystprep.com/study-notes/cfa-level-2/explain-the-use-of-value-at-risk-var-in-measuring-portfolio-risk/ (best)
- https://www.investopedia.com/terms/v/var.asp
- https://www.investopedia.com/financial-term-dictionary-4769738
- https://www.simtrade.fr/blog_simtrade/variance-covariance-method-var-calculation/ (must see)
- https://www.investopedia.com/terms/m/montecarlosimulation.asp (Monte-Carlo simulation)
- https://quantpy.com.au/risk-management/value-at-risk-var-and-conditional-var-cvar/
- https://analytica.com/monte-carlo-simulation-tips-and-tricks/ (check for later discussion)
- https://analytica.com/technology/monte-carlo-simulation-software/